Solveeit Logo
Login

Question

Question: The normal chord at a point t on the parabola \({{y}^{2}}=4ax\) subtends a right angle at the vertex...

The normal chord at a point t on the parabola y2=4ax{{y}^{2}}=4ax subtends a right angle at the vertex then t2{{t}^{2}} is equal to
(a) 4
(b) 2
(c) 1
(d) 3

Explanation

Solution

Hint: Assume that the chord is normal to the parabola at point P whose coordinate is given as P(at2,2at)P\left( a{{t}^{2}},2at \right). Now, let this chord meet the parabola again at Q whose coordinate is given by Q(at12,2at1)Q\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right). O is the origin and the vertex of the parabola y2=4ax{{y}^{2}}=4ax. Find a relation between t and t1{{t}_{1}} by equating the product of slopes of line OP and OQ equal to -1. Form another equation by the help of the general equation of normal to the parabola given by y=mx−am3−2amy=mx-a{{m}^{3}}-2am, where m is the slope of normal PQ. Solve the two equations to get the value of t2{{t}^{2}}.

Complete step-by-step solution -
__
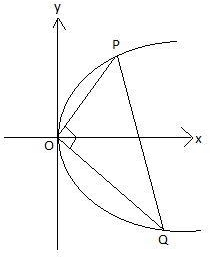
We know that, if two lines are perpendicular to each other then the product of their slopes is equal to −1-1. In the above question, since PQ subtends a right angle at the vertex of parabola, that is origin, therefore, OP and OQ are perpendicular.
Slope of line OP =ΔyΔx=2at−0at2−0=2t=\dfrac{\Delta y}{\Delta x}=\dfrac{2at-0}{a{{t}^{2}}-0}=\dfrac{2}{t}
Slope of line OQ =ΔyΔx=2at1−0at12−0=2t1=\dfrac{\Delta y}{\Delta x}=\dfrac{2a{{t}_{1}}-0}{a{{t}_{1}}^{2}-0}=\dfrac{2}{{{t}_{1}}}
Taking the product of slopes, we get,
2t×2t1=−1 ⇒tt1=−4....................(i) \begin{aligned} & \dfrac{2}{t}\times \dfrac{2}{{{t}_{1}}}=-1 \\\ & \Rightarrow t{{t}_{1}}=-4....................(i) \\\ \end{aligned}
Now, since PQ is a normal to the parabola and the general equation of a parabola is y=mx−am3−2amy=mx-a{{m}^{3}}-2am, where m is the slope of normal PQ.
Since, the line PQ passes through P(at2,2at)P\left( a{{t}^{2}},2at \right), therefore, substituting the coordinates in y=mx−am3−2amy=mx-a{{m}^{3}}-2am, we get,
2at=mat2−am3−2am ⇒am3+2am−amt2+2at=0 ⇒m3+2m−mt2+2t=0 \begin{aligned} & 2at=ma{{t}^{2}}-a{{m}^{3}}-2am \\\ & \Rightarrow a{{m}^{3}}+2am-am{{t}^{2}}+2at=0 \\\ & \Rightarrow {{m}^{3}}+2m-m{{t}^{2}}+2t=0 \\\ \end{aligned}
Substituting m = -t in the above equation, we get,
(−t)3+2(−t)−(−t)t2+2t =−t3−2t+t3+2t =0 \begin{aligned} & {{\left( -t \right)}^{3}}+2\left( -t \right)-\left( -t \right){{t}^{2}}+2t \\\ & =-{{t}^{3}}-2t+{{t}^{3}}+2t \\\ & =0 \\\ \end{aligned}
Therefore, ‘-t’ is the slope of line PQ.
Also, slope of the line PQ =ΔyΔx=2at−2at1at2−at12=2a(t−t1)a(t2−t12)=2a(t−t1)a(t−t1)(t+t1)=\dfrac{\Delta y}{\Delta x}=\dfrac{2at-2a{{t}_{1}}}{a{{t}^{2}}-a{{t}_{1}}^{2}}=\dfrac{2a(t-{{t}_{1}})}{a\left( {{t}^{2}}-{{t}_{1}}^{2} \right)}=\dfrac{2a(t-{{t}_{1}})}{a\left( t-{{t}_{1}} \right)\left( t+{{t}_{1}} \right)}
Cancelling the common terms, we get,
Slope of line PQ =2(t+t1)=\dfrac{2}{(t+{{t}_{1}})}
Therefore, equating (-t) with 2(t+t1)\dfrac{2}{(t+{{t}_{1}})}, we have,
2(t+t1)=−t ⇒−t2−tt1=2...................(ii) \begin{aligned} & \dfrac{2}{(t+{{t}_{1}})}=-t \\\ & \Rightarrow -{{t}^{2}}-t{{t}_{1}}=2...................(ii) \\\ \end{aligned}
Substituting the value of tt1t{{t}_{1}} from equation (i) in equation (ii), we get,
−t2−(−4)=2 ⇒−t2+4=2 ⇒t2=2 \begin{aligned} & -{{t}^{2}}-\left( -4 \right)=2 \\\ & \Rightarrow -{{t}^{2}}+4=2 \\\ & \Rightarrow {{t}^{2}}=2 \\\ \end{aligned}
Hence, option (b) is the correct answer.

Note: One may note that the equation of normal to the parabola is a cubic equation in ‘m’ that means a total of three normal can be drawn from a point outside the parabola. We have used a hit and trial method to determine one of the values of ‘m’ in terms of ‘t’. The other two values of ‘m’ are of no use here because we are already getting a simplified relation between t and t1{{t}_{1}}.