Question

The normal at the point $P(a{p^2},2ap)$ meets the parabola ${y^2} = 4ax$ again at $Q(a{q^2},2aq)$ such that the lines joining the origin to $P{\text{ }}and{\text{ }}Q$ are at right angle. Then
(A) ${p^2} = 2$
(B) ${q^2} = 2$
(C) $p = 2q$
(D) $q = 2p$

Answer 1

As per the question, we have the coordinates of the given two points $P{\text{ }}and{\text{ }}Q$ , so first we will write the equation for both normal and parabola with respect to the both given points. And then we will find the slope of both the points with their origin separately. And then the both lines are perpendicular to each other, so we will follow the product of the slopes which is equals to -1. We will get our final equation.

Complete Step By Step Answer:
As per the question-
Given equation of parabola is:
${y^2} = 4ax$

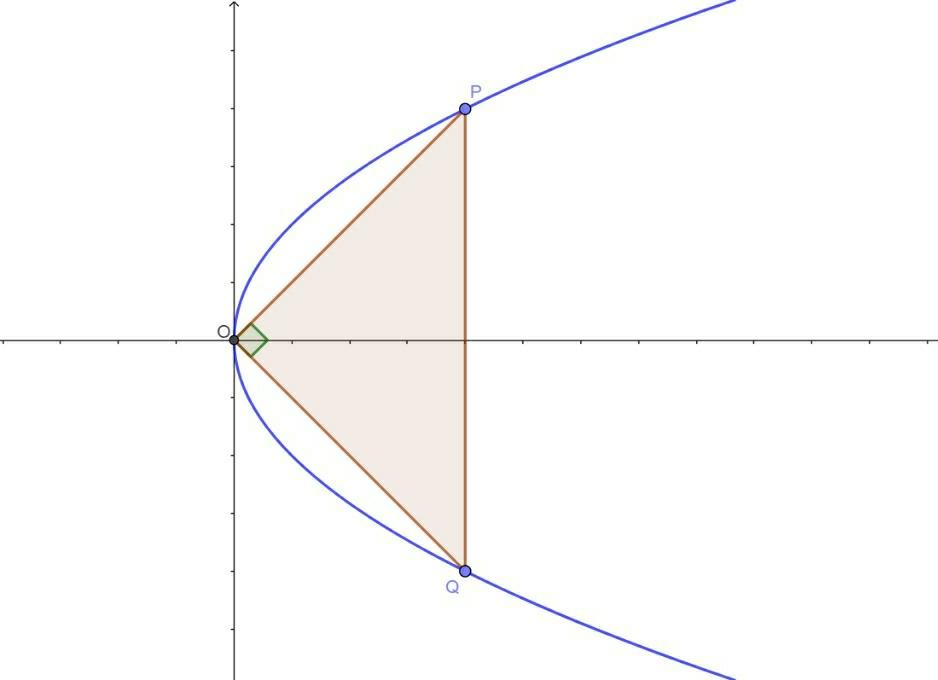
As we know the general equation of normal, at $P(a{p^2},2ap)$ is:
$\therefore y = - px + 2ap + a{p^3}$
Since, it meet the parabola again at $Q(a{q^2},2aq)$ is given by:
$q = - p - \dfrac{2}{p}$ ………eq(i)
So, from the origin $(O)$ -
We will find the slope between the origin and the point $P$ .
Slope of $OP = \dfrac{{2ap - 0}}{{a{p^2} - 0}} = \dfrac{2}{p}$
Similarly, we will find the slope between the origin and the point $Q$ :
Slope of $OQ = \dfrac{{2aq - 0}}{{a{q^2} - 0}} = \dfrac{2}{q}$
As we can see, both the lines are perpendicular to each other.
Since, $OP \bot OQ$ .
$\because {m_1}.{m_2} = - 1$
$\Rightarrow pq = - 4$
Using the equation(i) in the above equation:-
$\Rightarrow p( - p - \dfrac{2}{p}) = - 4 \\\ \Rightarrow {p^2} = 2 \\\$
Hence, the correct option is (A) ${p^2} = 2$ .

Note:
If and only if the product of their slopes is, two lines are perpendicular. To put it another way, the slope of a perpendicular line to a given line is the negative reciprocal of that slope. As a result, the line perpendicular to a line with a slope of 3 must be the negative reciprocal of 3.