Question

The normal at the point (3,4) on a circle cuts the circle at the point (-1,-2). Then the equation of the circle is
A) $x^{2}+y^{2}+2x-2y-13=0$
B) $x^{2}+y^{2}-2x-2y-11=0$
C) $x^{2}+y^{2}-2x+2y+12=0$
D) $x^{2}+y^{2}-2x-2y+14=0$

Answer 1

Hint: In this question it is given that the normal at the point (3,4) on a circle cuts the circle at the point (-1,-2). So we have to find the equation of the circle. So to understand it better we have to draw the diagram.

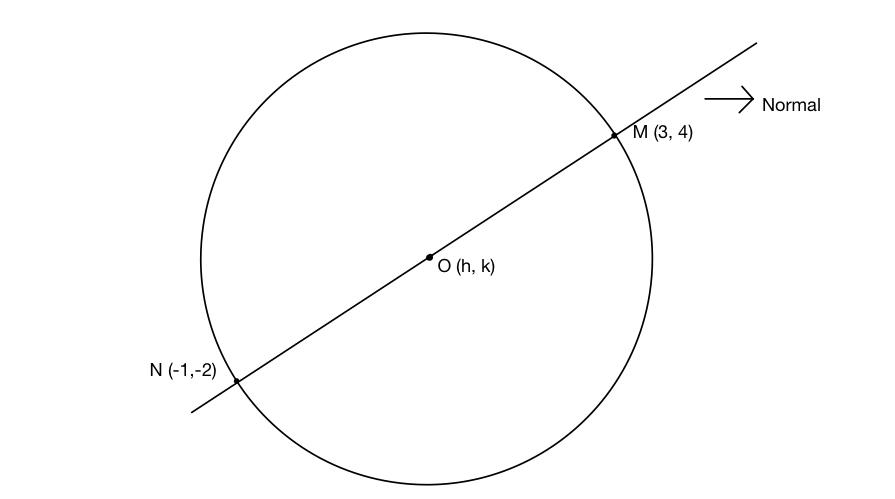
A normal line is always passing through the centre O(h,k) and intersect the circle at the end points of a diameter line, so to find the solution we have to find the centre of this circle O(h,k) which is the midpoint of (3,4) and (-1,-2) and the radius OM, after that we can easily find the equation of this circle.
Complete step by step answer:
As we know that a equation of a circle is in the form of,
$\left( x-h\right)^{2} +\left( y-k\right)^{2} =r^{2}$, ………(1)
Where, (h,k) is the is the centre of the circle and r is the radius.

Now we are going to find the coordinate of O(h,k), which is the midpoint of M and N. So to find the midpoint we have to know the midpoint formula which states that,
if (h,k) be the midpoint of (a,b) and (c,d), then we can write $h=\dfrac{a+c}{2} \ and\ k=\dfrac{b+d}{2}$.
So from the above formula we can write,
$h=\dfrac{3+\left( -1\right) }{2} \ and\ k=\dfrac{4+\left( -2\right) }{2}$
$\Rightarrow h=\dfrac{3-1}{2} \ and\ k=\dfrac{4-2}{2}$
$\Rightarrow h=1\ and\ k=1$.
So we get O(h,k)=(1,1).

Now radius r=OM.
For this we have to know the distance formula i.e, the distance between the points (a,b) to (c,d) is $\mathbf{d} =\sqrt{\left( a-c\right)^{2} +\left( b-d\right)^{2} }$ ............equation(2)
So from this we can write,
r=OM=$\sqrt{\left( 3-1\right)^{2} +\left( 4-1\right)^{2} }$=$\sqrt{2^{2}+3^{2}}$=$\sqrt{4+9}$=$\sqrt{13}$.

Now have got the centre (1,1) and the radius r=$\sqrt{13}$, so by (1) we can write the equation of circle,
$\left( x-1\right)^{2} +\left( y-1\right)^{2} =\left( \sqrt{13} \right)^{2}$
$\Rightarrow x^{2}-2x+1+y^{2}-2y+1=13$
$\Rightarrow x^{2}+y^{2}-2x-2y+2=13$
$\Rightarrow x^{2}+y^{2}-2x-2y+2-13=0$
$\Rightarrow x^{2}+y^{2}-2x-2y-11=0$
Which is the required equation of the circle.
Hence the correct option is option B.

Note: While solving this type of question you have to keep in mind that any normal line of a circle always passes through the centre of the circle. So to find the equation of a circle you only need to find the coordinate of centre and the radius of the circle. And the equation of circle will be $\left( x-h\right)^{2} +\left( y-k\right)^{2} =r^{2}$, where, (h,k) is the is the centre of the circle and r is the radius.