Question
Question: The normal at \( \left( {a,2a} \right) \) on \( {y^2} = 4ax \) meets the curve again at \( \left( {a...
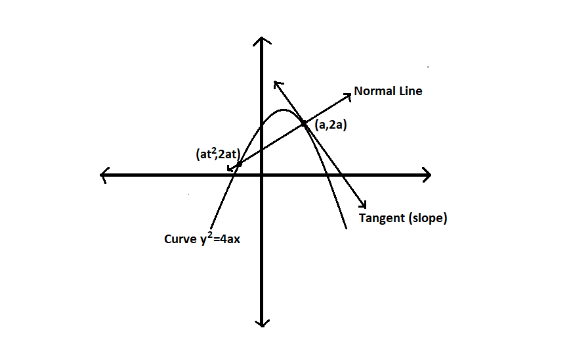
The normal at (a,2a) on y2=4ax meets the curve again at (at2,2at) . Then the value of its parameter is equal to
A. 1
B. 3
C. -1
D. -3
Solution
Hint : First find the slope of the tangent at point (a,2a) by differentiating the equation y2=4ax with respect to x. The slopes of perpendicular lines are negative reciprocals of one another. So using this, find the slope of normal at point (a,2a) as normal and tangent are perpendicular to each other. Using the slope of the normal line and point (a,2a) , find the line equation of the normal line. Substitute the line equation in the curve equation y2=4ax to find the parameter t.
Formulas used:
Slope-point form of a line equation is (y−y1)=m(x−x1) , where m is the slope and (x1,y1) is the given point.
Complete step by step solution:
We are given that the normal at (a,2a) on y2=4ax meets the curve again at (at2,2at) .
We have to find the value of t.
First we have to find the slope of tangent at point (a,2a) .
So we are differentiating y2=4ax with respect to x.
We get,
dxd(y2)=dxd(4ax)
⇒2ydxdy=4a(dxdx)
Let dxdy be y′ .
⇒2yy′=4a(∵dxdx=1)
⇒y′=2y4a
Slope of tangent at point (a,2a) is 2(2a)4a=4a4a=1 as y-coordinate of (a,2a) is 2a.
Tangent and normal are perpendicular lines. So the slope of the normal line at point (a,2a) is (1)−1=−1
We have got the slope of the normal and the point, (a,2a) , from which the normal travels.
Therefore, the equation of the normal line is (y−y1)=m(x−x1)
⇒y−2a=−1(x−a)
⇒y−2a=−x+a
⇒y=3a−x
On substituting the value of y as 3a−x in y2=4ax , we get
⇒(3a−x)2=4ax
⇒9a2+x2−6ax=4ax
⇒x2−6ax−4ax+9a2=0
⇒x2−10ax+9a2=0
We are next finding the factors of the above equation
⇒x2−ax−9ax+9a2=0
⇒x(x−a)−9a(x−a)=0
⇒(x−a)(x−9a)=0
∴x=a,x=9a
The value of x is 9a as we already know when x is a, y is 2a in the point (a,2a)
This gives,
y=3a−x=3a−9a=−6a
Therefore, the x and y coordinates of point (at2,2at) are 9a and -6a respectively.
This means that
⇒2at=−6a
∴t=2a−6a=−3
Therefore, the parameter t is equal to -3.
So, the correct answer is option (D), “ -3”.
Note : Here we have a slope and point given so we have used slope-point form to find the line equation of the normal. If two points of a line are given, then we have to use two-point form to find the line equation. A tangent is a straight line to a plane curve at a given point that just touches the curve only at one (given) point. Do not confuse a tangent with a secant.
