Question

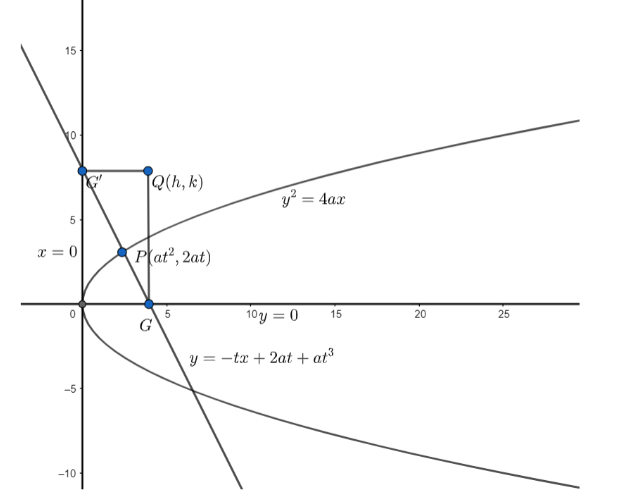
The normal at any point $P$ meets the axis in $G$ and the tangent at the vertex in ${{G}^{'}}$. If $A$ be the vertex and the rectangle $AGQ{{G}^{'}}$ be completed, prove that the equation of locus of $Q$ is
${{x}^{3}}=2a{{x}^{2}}+a{{y}^{2}}$

Answer 1

Hint:Here we use the property of a rectangle that the mid-points of the diagonals of a rectangle are the same .

Let’s consider the equation of the parabola to be ${{y}^{2}}=4ax$. So, its vertex is $A(0,0)$.
We know , any point on the parabola , given by the equation ${{y}^{2}}=4ax$, can be written as $P\left( a{{t}^{2}},2at \right)$.

Now , we will find the equation of normal to the parabola at $P$.
We know , the equation of the normal to the parabola in parametric form is given as
$y=-tx+2at+a{{t}^{3}}$
So, the equation of normal at $P$ can be written as
$y=-tx+2at+a{{t}^{3}}....\left( i \right)$
Now , we know , the axis of the parabola is $y=0$.
We need to find the point of intersection of the normal to the parabola and the axis of the parabola .
To find the point of intersection of normal and the axis , we will substitute $y=0$ in equation $\left( i \right)$.
On substituting $y=0$ in equation $\left( i \right)$ , we get
$0=-tx+2at+a{{t}^{3}}$
$\Rightarrow x=2a+a{{t}^{2}}$
So , the coordinates of $G$ are $\left( 2a+a{{t}^{2}},0 \right)$.
Now , we know , tangent to the parabola at vertex is given by the equation $x=0$.
So , the point of intersection of normal and tangent at vertex can be found by substituting $x=0$in $\left( i \right)$.
On substituting $x=0$in $\left( i \right)$, we get
$y=2at+a{{t}^{3}}$
So, ${{G}^{'}}=\left( 0,2at+a{{t}^{3}} \right)$
Now , since we need to find the locus of $Q$, let $Q=\left( h,k \right)$.
Now , it is given that $AGQ{{G}^{'}}$is a rectangle.
We know the diagonals of a rectangle bisect each other.
So , the midpoint of the diagonals $AQ$ and $G{{G}^{'}}$ is the same.
Now, we know that the coordinates of the midpoint of the line joining two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is given as: $\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$
So, midpoint of $AQ=\left( \dfrac{0+h}{2},\dfrac{0+k}{2} \right)$
$=\left( \dfrac{h}{2},\dfrac{k}{2} \right)....\left( ii \right)$
Midpoint of $G{{G}^{'}}=\left( \dfrac{2a+a{{t}^{2}}+0}{2},\dfrac{0+2at+a{{t}^{3}}}{2} \right)$
$=\left( \dfrac{2a+a{{t}^{2}}}{2},\dfrac{2at+a{{t}^{3}}}{2} \right)....\left( iii \right)$
Comparing $\left( ii \right)$ with $\left( iii \right)$,
$\dfrac{h}{2}=\dfrac{2a+a{{t}^{2}}}{2}\Rightarrow h=2a+a{{t}^{2}}....\left( iv \right)$
$\dfrac{k}{2}=\dfrac{2at+a{{t}^{3}}}{2}\Rightarrow k=2at+a{{t}^{3}}....\left( v \right)$
On dividing $\left( v \right)$by $\left( iv \right)$, we get
$\dfrac{k}{h}=\dfrac{2at+a{{t}^{3}}}{2a+a{{t}^{2}}}$
$\Rightarrow \dfrac{k}{h}=t$
Now, let’s substitute $t=\dfrac{k}{h}$in $\left( iv \right)$. We get ,
$h=2a+a{{\left( \dfrac{k}{h} \right)}^{2}}$
$\Rightarrow h=\dfrac{2a{{h}^{2}}+a{{k}^{2}}}{{{h}^{2}}}$
Or, ${{h}^{3}}=2a{{h}^{2}}+a{{k}^{2}}........$equation$(vi)$
Now, to find the locus of $Q\left( h,k \right)$, we will substitute $(x,y)$in place of $\left( h,k \right)$ in equation $(vi)$
So, the locus of $Q\left( h,k \right)$ is ${{x}^{3}}=2a{{x}^{2}}+a{{y}^{2}}$
Note: Vertex of ${{y}^{2}}=4ax$is $\left( 0,0 \right)$.
Tangent at vertex is $x=0$
Equation of the axis is $y=0$.
Students generally get confused between the equation of tangent at vertex and the equation of axis.