Question
Question: The network resistance is connected to \( 16V \) battery with internal resistance of \( 1\Omega \) a...
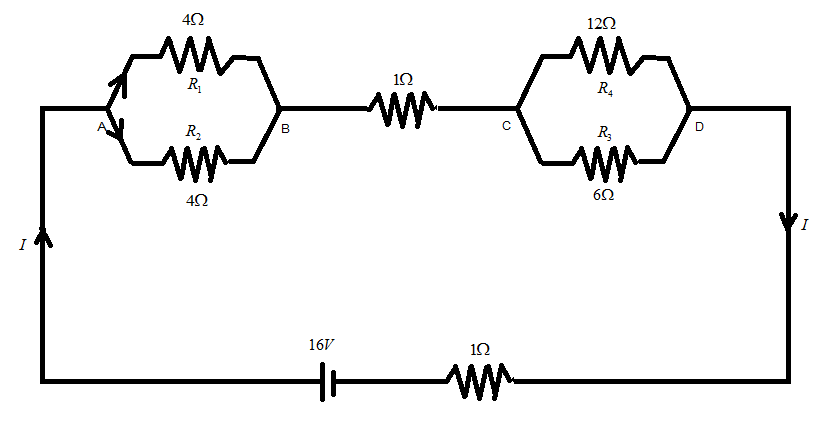
The network resistance is connected to 16V battery with internal resistance of 1Ω as shown in figure as:
1. Find equivalent resistance of the network.
2. Find current in each resistor.
3. Find voltage drops VAB , VBC , VCD .
Solution
We know that, when this type of circuit is given and we have to calculate the equivalent resistance, we have to solve it carefully using the formulas for resistances in parallel and series combination. For the resistances between A and B the current is divided into two equal parts since the resistances are of equal value i.e. the value of current depends on the value of resistance from which it is flowing.
Complete answer:
Let us first divide current in between A and B and C and D, and show it in the diagram such that as shown in the figure below:
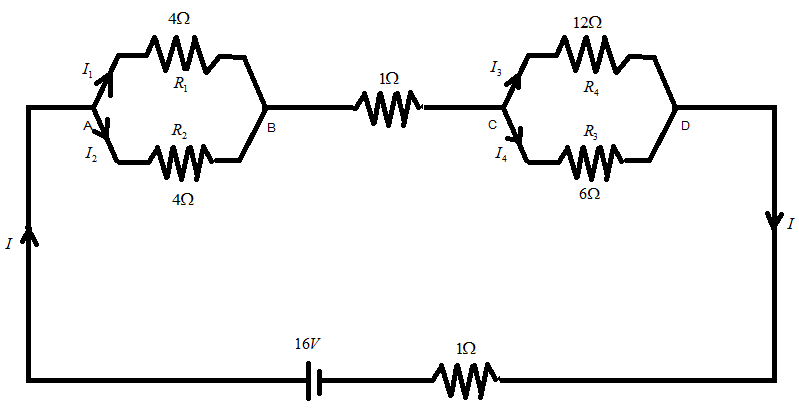
For (1),
We have, resistances in parallel between A and B, so we will use the formula for equivalent resistance in parallel as
Req=4+44×4=816=2Ω
Therefore, resistance between A and B is 2Ω .
Similarly between C and D,
Req=12+612×6=1872=4Ω
Therefore, resistance between C and D is 4Ω .
These all are in series now after solving the parallel resistances these resistances are now in parallel with the other two resistances such that 2Ω , 1Ω , 4Ω and 1Ω are in series in the above circuit.
Thus the equivalent resistance is given by the formula of the resistances in series combination is as follows in the whole network:
Req=2Ω+1Ω+4Ω+1Ω=8Ω
Hence, the equivalent resistance in the whole circuit is 8Ω .
For (2),
Current in each resistor,
Let us first divide the current flowing in each resistor such that current flowing from R1 is I1 , R2 is I2 , R3 is I3 and R4 is I4 .
I=I1+I2
∴I1=1A and I2=1A
The current moving out of the point B is 2A , this current is divided between two resistors equally but here the resistances are different so the currents are equal such that:
I3×12=I4×6
⇒I4=2I3
But, 2A=I3+I4
⇒I3=32A (by ohm’s law)
∴I4=34A
For (3),
Here, we have to find the voltage drops VAB , VBC , VCD .
By considering current flowing in any one of the resistors which are in parallel, we get
VAB=I1×4=1×4=4V (current from R1 between A and B)
Similarly, between B and C only one resistor is here so:
VBC=I×1=2×1=2V (current between B and C is 2A )
Now, for C and D,
VCD=I3×12=32×12=8V (current from R3 between C and D)
Hence, we have obtained all the answers.
Note:
In these types of circuit problems we must know that it is very important to understand the combinations of resistors if they are in parallel combination or in series combination. When the voltage drop is asked and not specified from which resistor just go for any one of them since the current will be equally distributed from the junction. Junction is the point where current is divided into two or more currents.
