Question
Question: The net resistance between X and Y is: (all resistances are in ohm) 
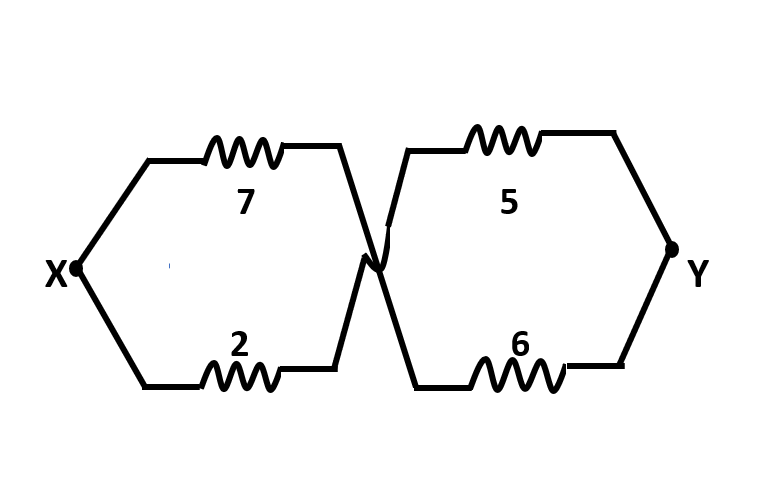
(A)4Ω(B)4.55Ω(C)2Ω(D)20Ω
Solution
The trick to this question lies in its figure only. The wire coming from 7ohm resistance is connected with 6ohm resistance and not 2ohm resistance. Also, the wire coming from 2ohm resistance is connected with the 5ohm resistance and not the 7ohm resistance. We shall use this fact to first simplify our circuit and then solve it to get the net resistance between X and Y.
Complete step-by-step solution:
Let us first simplify our circuit based on the above analysis. The simplified circuit is shown below (all resistances being in ohm):

Now, the resultant resistance between X and Y can be calculated easily.
Let the net resistance in the upper branch be R1 , then it is equal to:
⇒R1=(7+6)Ω⇒R1=13Ω
Now, let the resistance in the lower branch be given by R2, then it is equal to:
⇒R2=(5+2)Ω⇒R2=7Ω
Now, these two branches are connected across the same potential difference, this means they are connected in parallel. Hence, their net resistance could be calculated using the following formula:
⇒Rnet=R1+R2R1×R2
Putting the values of the two resistances, we get the equivalent resistance as:
⇒Rnet=13+713×7Ω⇒Rnet=2091Ω∴Rnet=4.55Ω
Hence, the net resistance between the points X and Y comes out to be 4.55Ω .
Hence, option (B) is the correct option.
Note: If we solve it ordinarily, then we will see that the 7 and 2, 5 and 6ohm resistances are in common. Now, this is where the problem lies. The wire through the 7ohm resistance trips below the wire coming from 2ohm resistance. We need to analyze these diagrams carefully and make sure to simplify our circuits if there are any complications.
