Solveeit Logo
Login

Question

Question: The net fore exerted on a particle acts in the +x direction. Its magnitude increases linearly from z...

The net fore exerted on a particle acts in the +x direction. Its magnitude increases linearly from zero at x = 0, to 24.0 N at x = 3.0 m. It remains constant at 24.0 N from x = 3.0m to x = 8.0m and then decreases linearly to zero at x = 13.0m. Determine the work done to move the particle from x = 0 to x = 13.0.

A

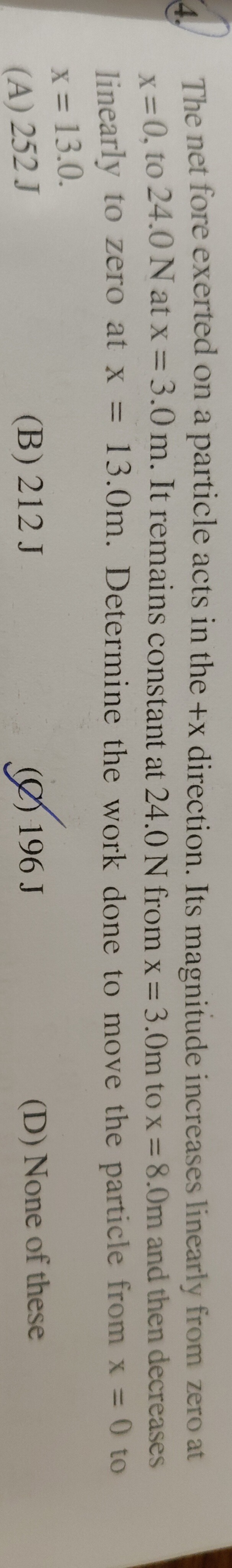
252 J

B

212 J

C

196 J

D

None of these

Answer

216 J

Explanation

Solution

The work done by a variable force is given by the area under the Force-displacement (F-x) graph. We can divide the given force profile into three distinct segments and calculate the work done in each segment.

1. Segment 1: From x = 0 m to x = 3.0 m

The force increases linearly from 0 N at x = 0 m to 24.0 N at x = 3.0 m. This segment forms a triangle on the F-x graph.

  • Base of the triangle = 3.0 m - 0 m = 3.0 m
  • Height of the triangle = 24.0 N
  • Work done (W1W_1) = Area of the triangle = 12×base×height\frac{1}{2} \times \text{base} \times \text{height}

W1=12×3.0 m×24.0 N=36 JW_1 = \frac{1}{2} \times 3.0 \text{ m} \times 24.0 \text{ N} = 36 \text{ J}

2. Segment 2: From x = 3.0 m to x = 8.0 m

The force remains constant at 24.0 N. This segment forms a rectangle on the F-x graph.

  • Width of the rectangle = 8.0 m - 3.0 m = 5.0 m
  • Height of the rectangle = 24.0 N
  • Work done (W2W_2) = Area of the rectangle = width×height\text{width} \times \text{height}

W2=5.0 m×24.0 N=120 JW_2 = 5.0 \text{ m} \times 24.0 \text{ N} = 120 \text{ J}

3. Segment 3: From x = 8.0 m to x = 13.0 m

The force decreases linearly from 24.0 N at x = 8.0 m to 0 N at x = 13.0 m. This segment forms another triangle on the F-x graph.

  • Base of the triangle = 13.0 m - 8.0 m = 5.0 m
  • Height of the triangle = 24.0 N
  • Work done (W3W_3) = Area of the triangle = 12×base×height\frac{1}{2} \times \text{base} \times \text{height}

W3=12×5.0 m×24.0 N=60 JW_3 = \frac{1}{2} \times 5.0 \text{ m} \times 24.0 \text{ N} = 60 \text{ J}

Total Work Done:

The total work done to move the particle from x = 0 m to x = 13.0 m is the sum of the work done in all three segments.

Wtotal=W1+W2+W3W_{\text{total}} = W_1 + W_2 + W_3

Wtotal=36 J+120 J+60 J=216 JW_{\text{total}} = 36 \text{ J} + 120 \text{ J} + 60 \text{ J} = 216 \text{ J}

The calculated work done is 216 J, which is not among options (A), (B), or (C). Therefore, the correct option is (D).