Question
Question: The net external force acting on the disk when its centre of mass is at displacement x with respect ...
The net external force acting on the disk when its centre of mass is at displacement x with respect to its equilibrium position is
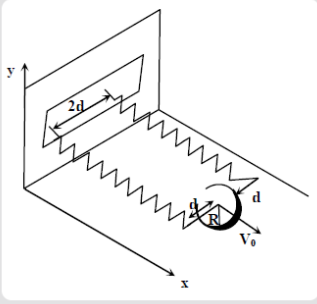
Solution
Net Force acting on a body is given by the formula:
FNet=m.a\lower0.5em⇀
Where,
FNet is the net force acting on the body
m is the mass of the body
a\lower0.5em⇀ is the acceleration of the body
Moment of Force is called Torque.
Net Torque acting on a body is given by the formula,
τNet=Iα
Where,
τNet is the net Torque acting on the body
I is the moment of inertia of the body
αis the angular acceleration of the body
Also,
τNet=F×R
Moment of inertia of a disk is given by the formula,
I=21MR2
Using all the above formulas, we can easily compute the result.
Complete step by step solution: Net Force acting on a body is given by the formula:
FNet=m.a\lower0.5em⇀
Where,
FNet is the net force acting on the body
m is the mass of the body
a\lower0.5em⇀ is the acceleration of the body
We will insert (−2kx+F)in the place of FNet
−2kx+F=Mac Equation 1
Where,
k is the spring constant
x is the distance by which the spring has been stretched
F is the friction force on the disk
M is the mass of disk
ac is the acceleration of centre of mass of the disk
Net Torque acting on a body is given by the formula,
τNet=Iα Equation 2
Where,
τNet is the net Torque acting on the body
I is the moment of inertia of the body
αis the angular acceleration of the body
Additionally, Torque is also calculated as follows,
τNet=F×R Equation 3
Where,
R is the distance of the Force from the centre of mass of the body
Now combining equations 2 and 3,
We get,
F×R=Iα
F=RIα Equation 4
In Pure Rolling condition,
ac=αcR
Moment of inertia of a disk is given by the formula,
I=21MR2
Inserting the values of α and I in equation 4,
We get,
F=R21MR2×Rac
=>F=21Mac
Inserting the value of F in equation 1,
We get,
=>−2kx+21Mac=−Mac
=>21Mac+Mac=2kx
=>23Mac=2kx
=>Mac=34kx
=>Mac=−34kx
Hence, Option (D) is correct.
Note:
We have used a negative sign because the disk has been displaced away from the equilibrium position. Hence this force will tend to bring the disk back to its initial position.
