Question

The mutual inductance between two coils is $0.15H$. If a current of $20A$ in the primary coil is cut off in $0.05s$, find the emf induced in the secondary coil. If the secondary coil has $60$ turns, then find the flux change in it.

Answer 1

The emf induced in a secondary coil due to change in current in the primary coil depends on the mutual inductance between the coils and the rate of change of current. Substituting corresponding values in the relation, we can calculate the emf induced. The change in flux depends on change in current and mutual inductance; we can substitute corresponding values to calculate flux.
Formulas used:
$e=-M\dfrac{\Delta I}{\Delta t}$
$\phi =M\Delta I$

Complete step-by-step solution:
The emf induced in the secondary coil due to current in the primary coil is given by-
$e=-M\dfrac{\Delta I}{\Delta t}$
Here, $e$ is the emf induced
$M$ is the mutual inductance between the coils
$\Delta I$ is the change in current
$\Delta t$ is the change in time

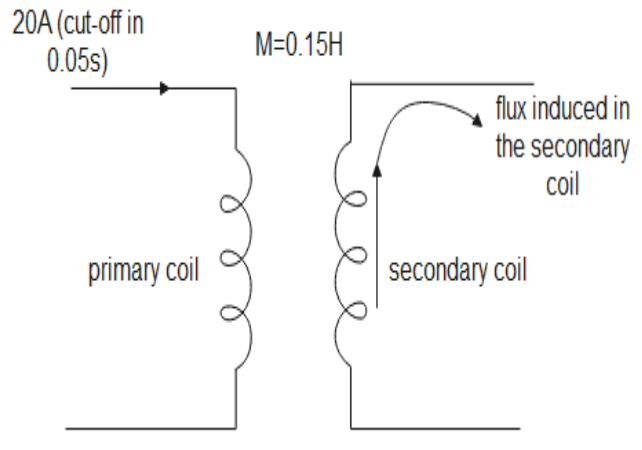
Given, mutual inductance between two coils is $0.15H$, initial current in primary coil is $20A$ and the final current is 0. Therefore, change in current will be $\Delta I=0-20= -20A$ and $\Delta t=0.05s$
Substituting given values in the above equation, we get,
$\begin{aligned} & e=-0.15\dfrac{-20}{0.05} \\\ & \therefore e=60V \\\ \end{aligned}$
Therefore, the emf induced in the secondary coil is $60V$.
The change in flux in secondary coil is given by-
$\phi =M\Delta I$
Here, $\phi$ is the change in flux
We substitute given values in the above equation to get,
$\begin{aligned} & \phi =0.15\times -20 \\\ & \Rightarrow \phi =-3Wb \\\ \end{aligned}$
Therefore, the change in flux in the secondary coil is $-3Wb$. The negative flux indicates that the change in flux opposes the change in current in the secondary coil.
Therefore, the emf induced in the secondary coil due to change in current in the primary coil is $60V$ and the magnitude of flux change in the primary coil is $3Wb$.

Note: The emf induced is negative because it opposes the change of current in the primary coil. The emf induced or change in flux is independent of the number of turns in primary or secondary coil. The mutual inductance of a coil depends on the change in flux and the change in current.