Question

The motion of a sphere moving on a rough horizontal surface changes from pure sliding (without rolling) to pure rolling (without slipping). In this process, the force of friction:
(A) Initially acts opposite to the direction of motion and later in the direction of motion
(B) Causes linear retardation
(C) Causes angular acceleration
(D) Stops acting when pure rolling begins

Answer 1

Hint
To solve this question, we need to examine the force of friction in the two kinds of motion of the sphere, pure sliding and pure rolling. As we know that the friction opposes the relative motion between the surfaces in contact, check for the relative motion between the surface of the sphere and the horizontal surface in each case.

Complete step by step answer

In the case of pure sliding, the bottom most point of the sphere slides along the horizontal surface. So, there is relative motion between the horizontal surface and the area of contact of the sphere. As we know that the force of friction opposes the relative motion between two surfaces in contact, so to oppose this relative motion, the frictional force will act opposite to the direction of motion of the sphere.
As shown in the above figure, the velocity of the sphere is in the right. So friction will act in the left. We know from Newton’s second law of motion that the direction of acceleration is the same as that of the force. So the acceleration of the sphere will also be in the left. As velocity and acceleration are in opposite directions, this is the case of linear retardation.
Thus, the friction will cause linear retardation in pure sliding.
So, option B is correct.
As we can see in the above figure, the frictional force also applies a torque, $\tau = fR$. Due to this torque, an angular acceleration is provided to the wheel.
So, option C is correct.
Also, due to this torque, the pure translational motion of the motion is converted to pure rolling motion.

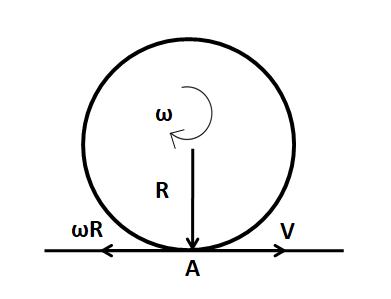
For pure rolling, the point A which is in contact with the surface must be at rest on the surface. From the above figure, this implies that $v = \omega R$. This means that the velocity of the point (A) is equal to zero. So, there is no relative motion between the surface of contact of the sphere and the horizontal surface, which makes the friction equal to zero.
Thus, the frictional force is absent when pure rolling begins.
So, option D is correct and at the same time option A is incorrect.
Hence, options B, C and D are correct.

Note
It is a common misconception that friction always opposes the motion of an object. Like in this question, you think that the friction should also oppose the pure rolling of the sphere. But this is not true. Instead, the concept of friction is based on the relative motion between the surfaces in contact only. Friction only comes into picture to oppose this relative motion, not to oppose the motion of any object.