Solveeit Logo
Login

Question

Question: The motion of a particle is given by y=a sin\(\omega t\) . What would be the time period of motion f...

The motion of a particle is given by y=a sinωt\omega t . What would be the time period of motion for this particle?
A) T=π2ω\dfrac{\pi }{{2\omega }}
B) T=πω\dfrac{\pi }{\omega }
C) T=2πω\dfrac{{2\pi }}{\omega }
D) T=4πω\dfrac{{4\pi }}{\omega }

Explanation

Solution

SHM Simple Harmonic Motion. The solution lies in the equation of the SHM. In SHM the particle moves from mean position to +A then again to mean position and after that toward –A and come back to its original point. It keeps oscillating but covers in 2π2\pi time.

Step by step solution:
Step 1:
Before considering the SHM, have a look on the image and it will clear the vision on how particle oscillate

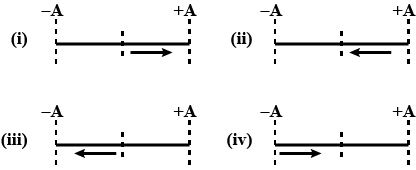
Step 2:
In (i) situation it is clearly visible that particle is at mean position and just started its oscillation, whenever a particle just starts its oscillation then it has no phase difference that means ϕ\phi is zero
In the first case the particle starts from the rest and goes to the extreme position +A . In part II it is returning from the extreme position, we can infer from this that the particle has a phase difference this time now.
The phase difference this time will be equal to π\pi because whenever a particle comes from the extreme position it has a phase difference equal to π\pi . Positive and negative signs depend on where it is coming from.
In (iii) this time from the origin to +A particle has covered A distance and then returned back to the mean position that means again a distance of A and now it is going to –A which is again at a distance of A from the mean position.
This time the phase distance will be equal to 3A and for this the phase difference will be equal to 3π2\dfrac{{3\pi }}{2}
In (iv) the particle returning from the extreme position of –A and phase will be 2π2\pi
From above statements we can rewrite it as, ωT\omega T =2π2\pi or T =2πω\dfrac{{2\pi }}{\omega }

That means Time period will be equal to 2πω\dfrac{{2\pi }}{\omega } . So, Option C. is correct.

Note: In simple harmonic motion the curve travels a sine graph. It starts from the rest at zero position and then continues its oscillation until it has energy.
All the oscillations are simple harmonic motion but all the simple harmonic motion can’t be said as oscillatory motion.