Question
Question: The mosquito net over a 7 ft \(\times\) 4 ft is 3 ft high. The net has a hole at one corner of the b...
The mosquito net over a 7 ft × 4 ft is 3 ft high. The net has a hole at one corner of the bed through which a mosquito enters the net. It flies and sits at the diagonally opposite upper corner of the net. Find the magnitude of the displacement of the mosquito, taking the hole as the origin. The length of the bed as the X-axis it, its width as the Y-axis and vertically up as the Z-axis is:
(A) 74ft
(B) 64ft
(C) 84ft
(D) 50ft
Solution
Hint We should know that to find the displacement factor in case of two points then we have to first find the coordinates of the displacement vectors. Then we have to move the second displacement vector so it starts where the first displacement vector has ended. At the end we have to draw the new vector that is the addition of the two displacement vectors.
Complete step by step answer
To write the answer we need to draw the diagram for the question. So here the diagram:
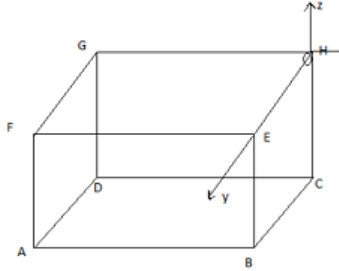
We know that here hole is at the corner H. So, the magnitude of the displacement of the mosquito is given by:
HA = 12+b2+c2
HA = 72+42+32
HA = 49+16+9=74ft
From the diagram the coordinates of point A is (-7, 3, -4).
So, the displacement vector is given by:
HA=−7i^+3k^−4k^
Hence, we can say that the components of the displacement vector are 7 ft, 3 ft and 4 ft respectively.
Note: We should know that in case of two-dimensional motion, the motion in a straight-line position of a point is represented by a vector which is known as the position vector of that specific point from a reference point. Whenever the body changes its position, the displacement happens, which is also a vector.
