Question

The monkey B as represented in the diagram is holding on to the tail of the monkey A which is climbing up a rope. The masses of the monkey A and B are given as $5kg$ and $2kg$ respectively. When the monkey A can withstand a tension of $30N$ in its tail, what will be the amount of force it must apply on the rope in order to carry the monkey B with it? Let us assume that $g=10m{{s}^{-2}}$.

$\begin{aligned} & A.\text{between }50N\text{ and }80N \\\ & B.\text{between }30N\text{ ad }80N \\\ & C.\text{between }70N\text{ ad }105N \\\ & D.\text{between }60N\text{ ad }90N \\\ \end{aligned}$

Answer 1

The maximum acceleration with which both can move upwards as a combined system should be found. When the acceleration becomes larger than this value, the tail of monkey A will break. Now the force which monkey A should provide on the rope such that monkey A gets this force experienced upon him as the reaction force should be sufficient to lift the monkey A and the child monkey B with a similar acceleration.

Complete step by step solution:
The monkey B who is the child of monkey A will be stationary with respect to the monkey A, and both moves with some similar acceleration $a$.

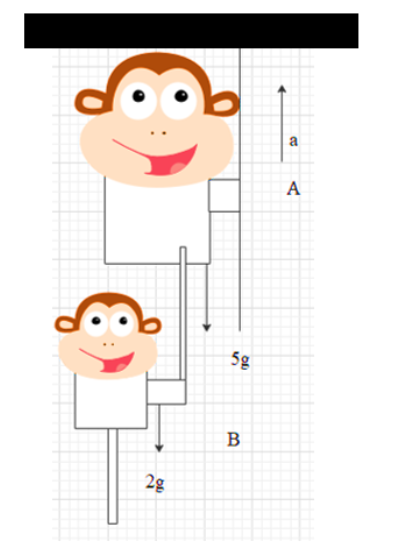
Now, the force with which monkey B must be pulled upwards in order to be lifted with acceleration$a$, the value should be identical to, $m\left( g+a \right)$, where $m$ be the mass of monkey B. As the maximum tension in the tail of monkey A can be $30N$.
Therefore we can write that,
$\begin{aligned} & 30=m\left( g+a \right)=2\left( 10+a \right) \\\ & \Rightarrow a=5m{{s}^{-2}} \\\ \end{aligned}$
This will be the maximum acceleration with which both can move upwards as a combined system. When the acceleration becomes larger than this value, the tail of monkey A will break. Now the force which monkey A should provide on the rope such that monkey A gets this force experienced upon him as the reaction force should be sufficient to lift the monkey A and the child monkey B with the similar acceleration of $5m{{s}^{-2}}$.
${{F}_{\max }}=\left( M+m \right)\left( g+a \right)=7\times 15=105N$
This will be the maximum force with which monkey A must pull the rope so that the combined system will move with maximum acceleration. The condition of the minimum force experienced on the combined system of the monkey and child will arise if both move up with zero acceleration. In such situation,
${{F}_{\min }}=\left( M+m \right)g=70N$

Thus the monkey A must pull the rope with the force of $70N$ to move up with maximum acceleration, so that the tension in his tail is just similar to the breaking strength of the tail.

Note: In physics, the tension can be defined as the pulling force which has been transmitted axially by the usage of a string, chain or a cable, or identical one-dimensional continuous body. The unit of the tension as well as its dimension is similar to that of the linear force.