Question

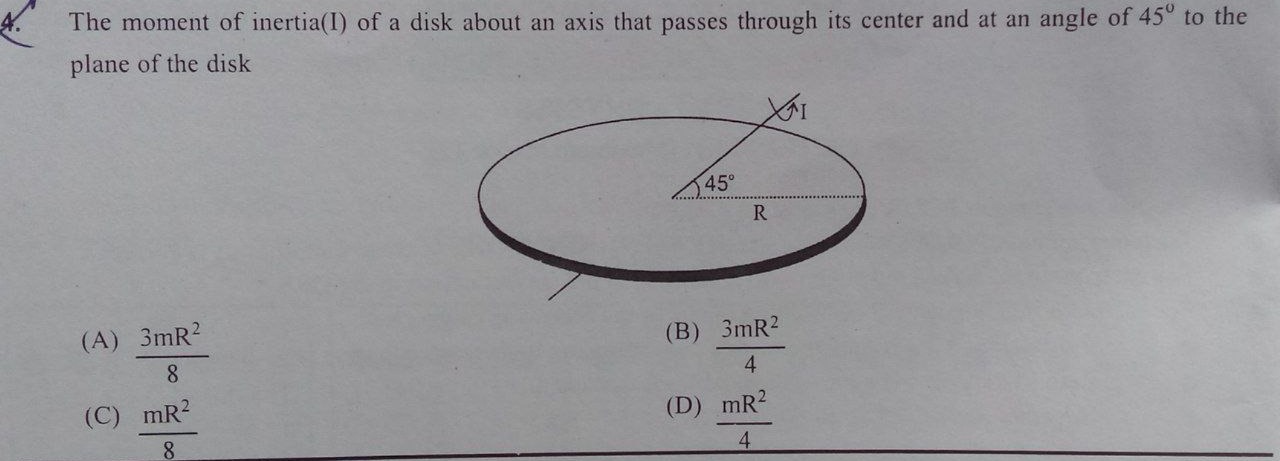
The moment of inertia(I) of a disk about an axis that passes through its center and at an angle of 45° to the plane of the disk

• A. $\frac{3mR^2}{8}$
• B. $\frac{3mR^2}{4}$
• C. $\frac{mR^2}{8}$
• D. $\frac{mR^2}{4}$

Answer 1

Answer: (A)

$\frac{3mR^2}{8}$

Answer 2

The moment of inertia of a uniform disk of mass $m$ and radius $R$ about an axis perpendicular to its plane and passing through its center is $I_{\perp} = \frac{1}{2}mR^2$. The moment of inertia about any diameter (an axis lying in the plane and passing through the center) is $I_{diam} = \frac{1}{4}mR^2$.

Let the axis of rotation be $L$. The problem states that $L$ passes through the center and makes an angle $\theta = 45^\circ$ with the plane of the disk. Let $\alpha$ be the angle between the axis $L$ and the normal to the plane of the disk. Then, $\alpha = 90^\circ - \theta$. Given $\theta = 45^\circ$, we have $\alpha = 90^\circ - 45^\circ = 45^\circ$.

The moment of inertia $I$ about an axis through the center of a planar body, making an angle $\alpha$ with the normal to the plane, is given by the formula: $I = I_{diam} \sin^2 \alpha + I_{\perp} \cos^2 \alpha$

Substitute the known values: $I_{diam} = \frac{1}{4}mR^2$ $I_{\perp} = \frac{1}{2}mR^2$ $\alpha = 45^\circ$, so $\sin \alpha = \frac{1}{\sqrt{2}}$ and $\cos \alpha = \frac{1}{\sqrt{2}}$. Therefore, $\sin^2 \alpha = \left(\frac{1}{\sqrt{2}}\right)^2 = \frac{1}{2}$ and $\cos^2 \alpha = \left(\frac{1}{\sqrt{2}}\right)^2 = \frac{1}{2}$.

Now, substitute these into the formula for $I$: $I = \left(\frac{1}{4}mR^2\right) \left(\frac{1}{2}\right) + \left(\frac{1}{2}mR^2\right) \left(\frac{1}{2}\right)$ $I = \frac{1}{8}mR^2 + \frac{1}{4}mR^2$ To add these terms, find a common denominator: $I = \frac{1}{8}mR^2 + \frac{2}{8}mR^2$ $I = \frac{3}{8}mR^2$

The moment of inertia of the disk about the given axis is $\frac{3mR^2}{8}$.