Question
Question: The moment of inertia of the pulley system as shown in the figure is \(3kg - {m^2}\). The radii of t...
The moment of inertia of the pulley system as shown in the figure is 3kg−m2. The radii of the bigger and smaller pulleys are 2m and 1m respectively. As the system is released from rest, find the angular acceleration of the pulley system (Assume that there is no slipping between string & pulley and string is light) [Take g=10m/s2]
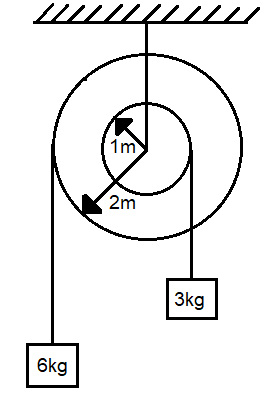
Solution
Hint
From the figure, we can determine the free body diagrams for both the blocks and find the free body equations for both the cases. From there we find the expressions for the tensions in both the strings. By substituting these tensions in the torque equations and writing the linear accelerations in terms of the angular accelerations we get the value of the angular acceleration.
In the solution to this question we will be using the following formula,
From the free-body diagrams,
⇒F−T=ma
Where F is the force and T is the tension on the string.
and the torque equation,
⇒T1r1−T2r2=Iα
Where T1 and T2 are the tensions in the two strings, ⇒r1 and r2 are the radius of the two pulleys.
I is the moment of inertia and α is the angular acceleration of the system.
Complete step by step answer
In this question, we are given a pulley system consisting of two pulleys and 2 masses.
let the mass of the bigger block be M=6kg
and mass of the smaller block, m=3kg
The radius of the bigger pulley is r1=2m
and the radius of the smaller pulley is r2=1m
So we can redraw the figure as,
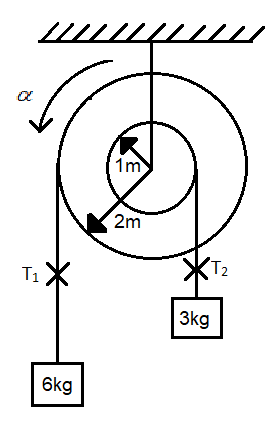
Now we draw the free body diagram of the blocks as follows,
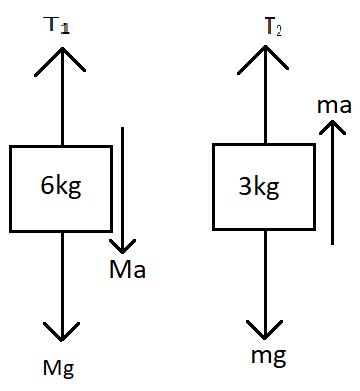
From the free-body diagrams, we get the equations of motion of the pulleys as,
⇒Mg−T1=Ma for the bigger block
Therefore, we can find the expression of T1 as,
⇒T1=Mg−Maand,
⇒T2−mg=ma for the smaller block
From here we can find the expression of T2 as,
⇒T2=mg+ma
Now for the pulley, the torque equation is given by,
⇒T1r1−T2r2=Iα
Here we can substitute the expressions of the tensions as,
⇒(Mg−Ma)r1−(mg+ma)r2=Iα
Here a is the linear accelerations of the blocks. So we can write the linear acceleration in terms of the angular acceleration as,
⇒a=r1α for the bigger block and a=r2α for the smaller block. Therefore substituting we get,
⇒[Mg−M(r1α)]r1−[mg+m(r2α)]r2=Iα
Now substituting the values of the masses and the radii we get,
⇒[6g−6(2α)]2−[3g+3(α)]=Iα
On opening the brackets we get,
⇒12g−24α−3g−3α=Iα
In the question, the value of the moment of inertia of the pulley system is given, I=3kg−m2.
Substituting this value we get,
⇒12g−24α−3g−3α=3α
taking α common we have,
⇒12g−3g=3α+24α+3α
⇒9g=30α
Therefore the value of angular acceleration is,
⇒α=309g
Putting the value of g=10m/s2
⇒α=309×10=3rad/s2
So the angular acceleration of the system is α=3rad/s2.
Note
The moment of inertia is the rotational equivalent of the mass in linear motion. It is the tendency of the body to resist angular acceleration. It is calculated by the sum of the product of the masses of each particle and their distance from the axis of rotation.
