Question

The moment of inertia of the plate about Z-axis is

(A) $\dfrac{M{{L}^{2}}}{12}$
(B) $\dfrac{M{{L}^{2}}}{24}$
(C) $\dfrac{M{{L}^{2}}}{6}$
(D) none of these

Answer 1

The moment of inertia of the plate around the Z-axis is not directly defined but the integration of the very small moment of inertia of small strips around the Z-axis will give the total moment of inertia. The triangle plate is isosceles so the height can be found by length $L$and the mass across the small strip can be found by area of the triangle.

Formula used:
Moment of inertia of rod: $I=\dfrac{M{{L}^{2}}}{12}$
And parallel axis theorem: $I'=I+M{{R}^{2}}$

Complete answer:
Moment of inertia of a given isosceles triangle can be determined by small stripes of the plate parallel to the X-axis shown in the figure below.

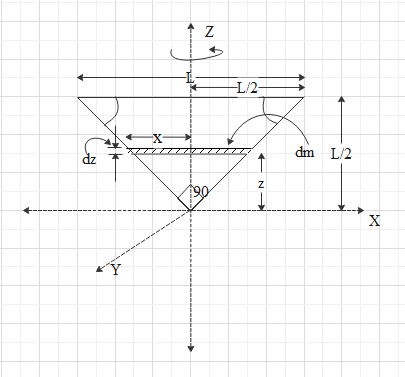
Assume a very small strip at distance $z$ from the origin. Here the length of the strip will be considered as$x$, the mass of the strip is $dm$ and the width of it is $dz$.
The mass of the strip can be found by area of the triangle,

& \text{mass of triangle }\to \text{ }area\text{ of triangle} \\\ & dm\text{ }\to \text{ ?} \\\ \end{aligned}$$ $$dm=\dfrac{4M}{{{L}^{2}}}(2xdz)$$ Now the moment of inertia of rod about its centre is $$I=\dfrac{M{{L}^{2}}}{12}$$ $$\therefore dI=\dfrac{dm{{(2x)}^{2}}}{12}+dm{{z}^{2}}$$ $$\therefore dI=\dfrac{{{(2x)}^{2}}}{12}\dfrac{4M}{{{L}^{2}}}(2xdz)+\dfrac{4M}{{{L}^{2}}}(2xdz){{z}^{2}}$$ But the triangle is isosceles $$\therefore x=z$$ because,  $$\therefore dI=\dfrac{{{(2z)}^{2}}}{12}\dfrac{4M}{{{L}^{2}}}(2zdz)+\dfrac{4M}{{{L}^{2}}}(2zdz){{z}^{2}}$$ $$\therefore dI=\dfrac{32}{3}\dfrac{M}{{{L}^{2}}}({{z}^{3}}dz)$$ Integrating both the side, $$\therefore \int{dI}=\dfrac{32}{3}\dfrac{M}{{{L}^{2}}}\int\limits_{0}^{{L}/{2}\;}{{{z}^{3}}dz}$$ $$\therefore I=\dfrac{M{{L}^{2}}}{6}$$ **So, the correct answer is “Option C”.** **Additional Information:** Moment of inertia is the measurement of the rotational inertia of a body. The opposition of the angular speed is a moment of inertia. Here the plate rotating about the Z-axis so the opposition in rotation is called moment of inertia if this triangle plate. **Note:** Direct moment of inertia of the triangle is not defined early but it should be calculated by the small help of calculus. The moment of inertia of the plate is the integral of a small component perpendicular to its rotation either parallel to X-axis or Y-axis. And the mass of that small component depends on the distribution of mass per unit area of the plate homogeneously.