Question
Question: The moment of inertia of the following structure about the axis XX’ made up of uniform thin wire of ...
The moment of inertia of the following structure about the axis XX’ made up of uniform thin wire of mass per unit length λ as shown in the figure is (all the double arrows indicate ‘l’ length) –
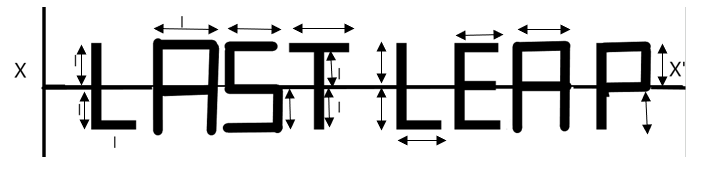
Solution
We need to find the moment of inertia with respect to each of the alignment used in the text in the questions. We have to use the formula for the perpendicular to the axis and the formula for parallel to the axis and add them all together.
Complete answer:
We know that the moment of inertia of a body is the mass about its origin or a point under consideration. The moment of inertia is generally the product of the mass and the square of the distance from the axis.
I=mr2
We are provided with a combination of masses about an axis. We need to find the moment of inertia of each element and add all the moments to get the required solution. We are also provided with the line density λ, which when multiplied by the length gives the mass.
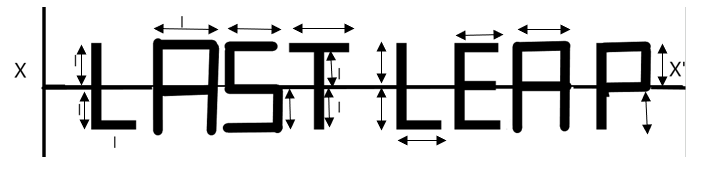
So, let us consider the masses which are parallel to the axis XX’ and that are not on the axis. The masses parallel to and on the axis don't have a moment about the axis.
There are 10 such masses at a distance ‘l’ from the axis. The moment of inertia of these are given by –
