Question

The moment of inertia of pulley is I and its radius is R. The string does not slip on the pulley as system is released then, the acceleration of the system is-

$\text{A}\text{. }\dfrac{g}{3+\dfrac{I}{m{{R}^{2}}}}$
$\text{B}\text{. }\dfrac{g}{1+\dfrac{I}{m{{R}^{2}}}}$
$\text{C}\text{. }\dfrac{3g}{1+\dfrac{I}{m{{R}^{2}}}}$
$\text{D}\text{. }\dfrac{3g}{2+\dfrac{I}{m{{R}^{2}}}}$

Answer 1

Write the equations of the net forces on the two blocks of masses m and 2m. The acceleration of the bodies and the pulley will be the same. Calculate the net torque on the pulley by using $\tau =Fr$. Then use $\tau =I\alpha$ and $a=R\alpha$. Perform some mathematical operations on the found equations and find a.
Formula used:
$\tau =Fr$
$\tau =I\alpha$
$a=R\alpha$

Complete answer:
As the system is released, both the blocks will move with accelerations of same magnitudes but opposite in the direction. The tension in the sections of the string on both the sides are ${{T}_{1}}$ and ${{T}_{2}}$, as shown in the figure.

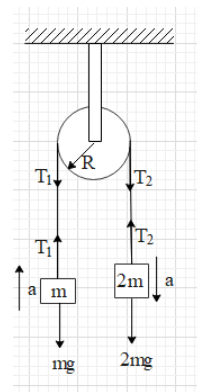
As we can see, there are two forces on the block of mass m. One is the gravitational force (mg) exerted by the earth, that is directed downwards. Another is the tension force (${{T}_{1}}$) acting upwards. The net force on this block will be ${{T}_{1}}-mg$.
From Newton’s second law of motion we get, ${{T}_{1}}-mg=ma$ …. (i).
On the block of mass 2m, the gravitational force acting downwards is equal to 2mg and the tension acting upwards is ${{T}_{2}}$.
Hence, $2mg-{{T}_{2}}=2ma$. …. (ii).
Let analyse the pulley. Since it is given that the string does not slip on the pulley, the pulley will have the same acceleration a.
The tension forces ${{T}_{1}}$ and ${{T}_{2}}$ are acting on the pulley as shown. Each of the tension forces will create a torque on the pulley and the pulley will rotate about its centre.
When a force F is tangential to the surface of a body, torque created by the force is $\tau =Fr$, where is the perpendicular distance of the point of rotation from the axis of force.
Therefore, the torque created by force ${{T}_{1}}$ is ${{\tau }_{1}}={{T}_{1}}R$ in anticlockwise direction.
And the torque created by force ${{T}_{2}}$ is ${{\tau }_{2}}={{T}_{2}}R$ in clockwise direction.
Since the torque are in opposite direction, the net torque on the pulley is $\tau ={{\tau }_{2}}-{{\tau }_{1}}={{T}_{2}}R-{{T}_{1}}R=\left( {{T}_{2}}-{{T}_{1}} \right)R$.
The net torque is also given as $\tau =I\alpha$, where I is the moment of inertia of the body about the axis of rotation and $\alpha$ is the angular acceleration of the body.
This means that $\tau =\left( {{T}_{2}}-{{T}_{1}} \right)R=I\alpha$
$\Rightarrow \alpha =\dfrac{\left( {{T}_{2}}-{{T}_{1}} \right)R}{I}$ …. (iii).
The acceleration of a circular disc (pulley) is given $a=R\alpha$.
Substitute the value of $\alpha$ from equation (iii).
$\Rightarrow a=R\left( \dfrac{\left( {{T}_{2}}-{{T}_{1}} \right)R}{I} \right)$ …. (iv).
Let us find the value of $\left( {{T}_{2}}-{{T}_{1}} \right)$.
Add (i) and (ii).
$\Rightarrow {{T}_{1}}-mg+2mg-{{T}_{2}}=ma+2ma$
$\Rightarrow {{T}_{1}}-{{T}_{2}}=3ma-mg$
$\Rightarrow {{T}_{2}}-{{T}_{1}}=mg-3ma$
Substitute the value of $\left( {{T}_{2}}-{{T}_{1}} \right)$ in equation (iv)
$\Rightarrow a=R\left( \dfrac{(mg-3ma)R}{I} \right)$
$\Rightarrow a=R\left( \dfrac{mgR-3maR}{I} \right)$
$\Rightarrow a=\left( \dfrac{mg{{R}^{2}}}{I}-\dfrac{3ma{{R}^{2}}}{I} \right)$
$\Rightarrow a+\dfrac{3ma{{R}^{2}}}{I}=\dfrac{mg{{R}^{2}}}{I}$
$\Rightarrow a\left( 1+\dfrac{3m{{R}^{2}}}{I} \right)=\dfrac{mg{{R}^{2}}}{I}$
$\Rightarrow a=\dfrac{\dfrac{mg{{R}^{2}}}{I}}{\left( 1+\dfrac{3m{{R}^{2}}}{I} \right)}=\dfrac{mg{{R}^{2}}}{I+3m{{R}^{2}}}=\dfrac{g}{\dfrac{I}{m{{R}^{2}}}+3}$.

Hence, the correct option is A.

Note:
Students may make a mistake by considering the same tension in both the sections.
Both the tensions will be the same when there is no friction between the string and the pulley. In that case, the pulley will not rotate.