Question
Question: The moment of inertia of an uniform thin sheet of mass M of the given shape about the specified axis...
The moment of inertia of an uniform thin sheet of mass M of the given shape about the specified axis is (axis and sheet both are in same plane):
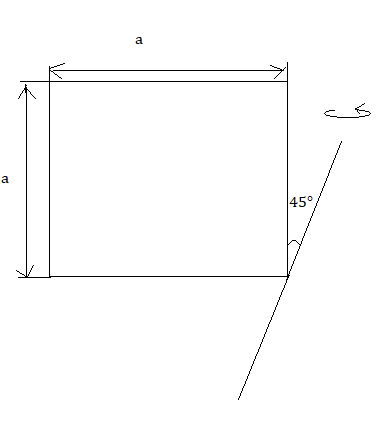
A. 27Ma2
B. 125Ma2
C. 31Ma2
D. 121Ma2
Solution
The moment of Inertia is denoted by I, measures the extent to which an object resists rotational acceleration about a particular axis, and is the rotational analogue to mass. Mass moments of inertia have units of dimension = ML2 ([mass] × [length]2).
The moment of the inertia of the sheet with respect to an axis perpendicular to the plane is
I=61Ma2.
Formula used: I=I1+I2 (perpendicular axis theorem) and I2=I1+Md2 (parallel axis theorem).
Complete step by step solution:
The moment of the inertia of the sheet with respect to an axis perpendicular to the plane is: -
I=61Ma2.
Let the moment of inertia of the diagonals of the sheets be I1 and I2 then according to perpendicular axis theorem, I=I1+I2
By symmetry, I1=I2=2I
I1=121Ma2
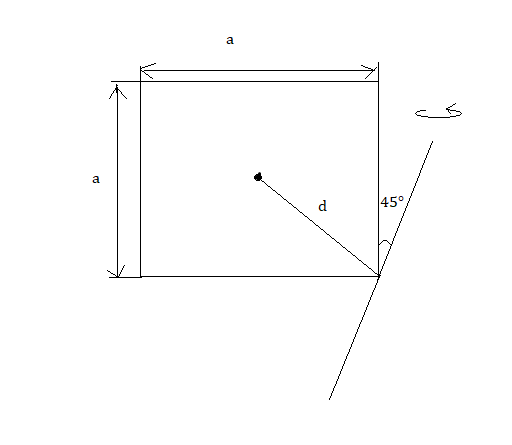
Now, using the parallel axis theorem, the moment of inertia of the given axis [i.e.,45∘ to the side] is,
I2=I1+Md2
[where, d=2a2 as shown in the figure beside]
