Question

The moment of inertia of a uniform circular disc of radius R and mass M about an axis passing from the edge of the disc and normal to the disc is:
(A) $M{R^2}$
(B) $\dfrac{1}{2}M{R^2}$
(C) $\dfrac{3}{2}M{R^2}$
(D) $\dfrac{7}{2}M{R^2}$

Answer 1

Hint : Moment of inertia is the name given to rotational inertia, the rotational analog of mass for linear motion. It appears in the relationships for the dynamics of rotational motion. The moment of inertia must be specified with respect to a chosen axis of rotation. For a point mass, the moment of inertia is just the mass times the square of perpendicular distance to the rotation axis, $I = \dfrac{1}{2}M{R^2}$ . That point mass relationship becomes the basis for all other moments of inertia since any object can be built up from a collection of point masses.

Complete Step By Step Answer:
We have the following diagram as stated in the question:

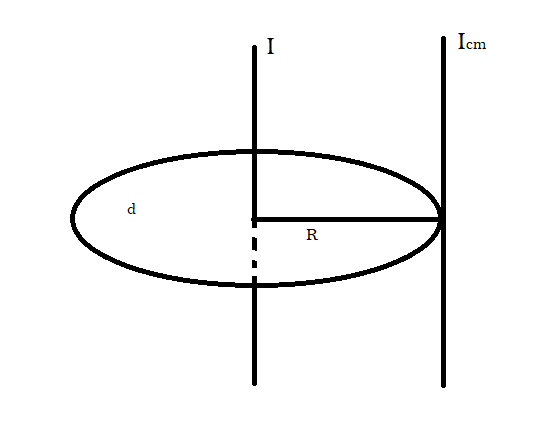
Here d is the disc of mass $M$ , $I$ is the axis passing through centre of mass, ${I_{cm}}$ is axis passing from the edge of the disc and normal to the disc, also it will be parallel to the axis passing through centre of mass and $R$ is the radius of the disc.
Now, The moment of inertia about an axis passing through centre of mass of disc and perpendicular to its plane is ${I_{cm}} = \dfrac{1}{2}M{R^2}$ where M is the mass of disc and R its radius. According to the theorem of parallel axis. According to parallel axis theorem the moment of inertia of any object about an axis through its centre of mass is the minimum moment of inertia for an axis in that direction in space. The moment of inertia about any axis parallel to that axis through the centre of mass is given by $M{R^2}$
${I_{parallel\,\,axis}} = {I_{cm}} + M{R^2}$
The expression added to the centre of mass moment of inertia will be recognized as the moment of inertia of a point mass - the moment of inertia about a parallel axis is the centre of mass moment plus the moment of inertia of the entire object treated as a point mass at the centre of mass.
So, the moment of inertia of circular disc about an axis touching the disc at its diameter and normal to the disc is given by
$I = {I_{cm}} + M{R^2}$
Substituting from above we have,
$\Rightarrow I = \dfrac{1}{2}M{R^2} + M{R^2}$
On simplifying we get,
$\Rightarrow I = \dfrac{3}{2}M{R^2}$
Hence option ‘C’ is correct.

Note :
Use of the parallel axis theorem is important. The question might be there with a different position of the axis and with a different mass of disc. In parallel axis theorem the shape of the disc doesn’t matter. Moment of inertia for both $I$ and ${I_{cm}}$ will be in an anticlockwise direction. If mass and radius changes then the moment of inertia will also change.