Question
Question: The moment of inertia of a uniform circular disc of radius \(R\) and mass \(M\) about an axis passin...
The moment of inertia of a uniform circular disc of radius R and mass M about an axis passing from the edge of the disc and normal to the disc is:
A.)MR2
B.)21MR2
C.)23MR2
D.)27MR2
Solution
Hint: The moment of inertia of a uniform circular disc about an axis passing through the edge of the disc and normal to the surface can be calculated using the parallel axis theorem and form the knowledge of the moment of inertia of the circular disc about an axis passing through its centre and perpendicular to the surface.
Formula used:
The parallel axis theorem states that the moment of inertia (Iparallel) of a body about an axis that is shifted parallel to another axis by a distance L is given by
Iparallel=I+ML2
where I is the moment of inertia of the body about the axis from which the shift has taken place to get the new axis and M is the mass of the body.
Complete step by step answer:
We can find out the moment of inertia of the uniform circular disc about an axis passing through its edge and normal to its surface by using the parallel axis theorem and the moment of inertia of the disc about the axis passing through its centre and normal to its surface.
The parallel axis theorem states that the moment of inertia (Iparallel) of a body about an axis that is shifted parallel to another axis by a distance L is given by
Iparallel=I+ML2 --(1)
where I is the moment of inertia of the body about the axis from which the shift has taken place to get the new axis and M is the mass of the body.
Therefore, let us analyze the question.
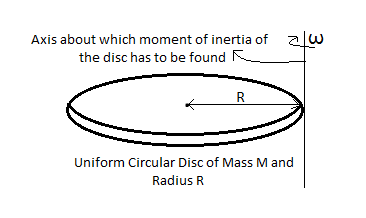
The mass of the disc is M and its radius is R.
The perpendicular distance between the edge of the disc and the centre will be nothing but the radius of the disc.
The moment of inertia of the disc about the axis passing through its centre and normal to its surface is I0=2MR2
Therefore, using this information in (1), we get the moment of inertia (I) of the disc about the axis normal to its surface and passing through its edge as,
I=I0+MR2
∴I=2MR2+MR2=23MR2
Hence, the required moment of inertia about the required axis is 23MR2.
Therefore, the correct option is C) 23MR2.
Note: Students must properly understand the parallel and perpendicular axis theorems as they are very important in solving almost all problems of rotational mechanics. This is because even if the student knows the moment of inertia about only one axis of a shape, they can easily find out the moment of inertia about other axes also using a combination of the parallel and perpendicular axis theorems.
Students must take care of the axis about which the moment of inertia is required. Usually, the moment of inertia of a body is different about different axes and hence, assuming the moment of inertia about a wrong axis will lead to a wrong value of the moment of inertia and eventually lead to a wrong answer.
ω
