Question

The moment of inertia of a thin uniform circular disc about one of its diameter is I. The moment of inertia about an axis perpendicular to the circular surface and passing through its center is
$(a){\text{ }}\sqrt 2 I \\\ (b){\text{ 2I}} \\\ {\text{(c) }}\dfrac{I}{2} \\\ (d){\text{ }}\dfrac{I}{{\sqrt 2 }} \\\$

Answer 1

Hint: In this question use the concept that diameter is always passing through the center of the circle so all the axis’s i.e. x, y and z are passing through the center of the circle which represents the diameter of the thin uniform circular disc in 3-D. Thus Moment of inertia about the z axis which is perpendicular to the circular surface and passing through its center will be the addition of moment of inertia about the x axis and moment of inertia about the y axis.

Complete step-by-step solution -

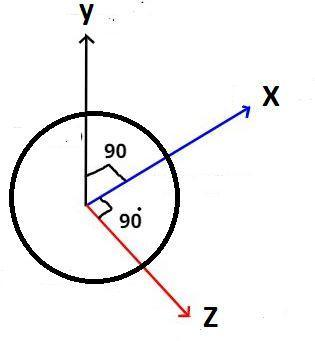
It is given that the moment of inertia of a thin uniform circular disc about one of its diameter is I.
If the diameter is about x axis so the moment of inertia about the x axis is ${I_x}$ and if the diameter is about y axis so the moment of inertia about the y axis is ${I_y}$.
Therefore, ${I_x} = {I_y} = I$
Now as we know that in 3 dimensional all the axes i.e. x, y and z are perpendicular to each other.
Now as we know that the diameter is always passing through the center of the circle so all the axis’s i.e. x, y and z are passing through the center of the circle which represents the diameter of the thin uniform circular disc in 3-D.
So the moment of inertia about an axis perpendicular to the circular surface and passing through its center is ${I_z}$.
Now according to the perpendicular axis theorem we have,
Moment of inertia about the z axis which is perpendicular to the circular surface and passing through its center = moment of inertia about the x axis + moment of inertia about the y axis.
Now substitute the values we have,
$\Rightarrow {I_z} = {I_x} + {I_y}$
$\Rightarrow {I_z} = I + I = 2I$
So this the required moment of inertia perpendicular to the circular surface and passing through its center.

Hence option (B) is the correct answer.

Note: A body has the tendency to resist angular acceleration, so moment of inertia is the measure of tendency of the body to resist this angular acceleration. In general moment of inertia is given as $I = \sum {{m_i}{r_i}^2}$ that is it is equal to the sum of the product of each element’s mass and the square of the distance of these elements from the axis about which moment of inertia has to be taken out.