Question

The moment of inertia of a square lamina about the perpendicular axis through its centre of mass is $20\,kg\,{m^2}$. Then its moment of inertia about an axis touching its side and in the plane of the lamina will be:
A. $10\,kg - {m^2}$
B. $30\,kg - {m^2}$
C. $40\,kg - {m^2}$
D. $25\,kg - {m^2}$

Answer 1

Use the perpendicular axis theorem to calculate the moment of inertia about the axis passing through the centre in the plane of the lamina. Use the perpendicular axes theorem to determine the moment of inertia about the axis touching the edge of the lamina in the plane of the lamina.

Formula used:
Theorem of parallel axes, $I = {I_C} + m{h^2}$
Here, ${I_C}$ is the moment of inertia about the central axis perpendicular to the plane, m is the mass of the object and h is the distance of the axis from the centre of mass.

Complete Step by Step Answer:
We have given that the moment of inertia of a square lamina about the perpendicular axis through its centre of mass is $20\,kg\,{m^2}$.

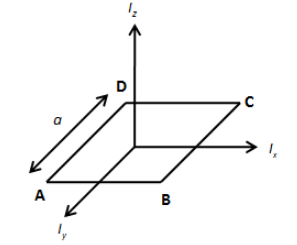
Applying the principle of perpendicular axes in the above diagram, we get,
${I_z} = {I_x} + {I_y}$
Since the square lamina has all the sides the same, the moment of inertia, ${I_x} = {I_y}$.
Therefore,
${I_z} = 2{I_x}$
$\Rightarrow {I_x} = \dfrac{{{I_z}}}{2}$
We have the expression for the moment of inertia of the square about its centre is,
${I_z} = \dfrac{{m{a^2}}}{6}$, where, a is the length of the side of the square lamina.
Therefore, the moment of inertia ${I_x}$ will be,
${I_x} = \dfrac{{m{a^2}}}{{12}}$ …… (1)

Now, let us use the principle of parallel axes as follows,
${I_{AB}} = {I_x} + m{\left( {\dfrac{a}{2}} \right)^2}$
Here, $\dfrac{a}{2}$ is the distance of the axis AB from the centre.
Using equation (1) in the above equation, we get,
${I_{AB}} = \dfrac{{m{a^2}}}{{12}} + \dfrac{{m{a^2}}}{4}$
$\Rightarrow {I_{AB}} = \dfrac{{m{a^2}}}{3}$
$\Rightarrow {I_{AB}} = 2 \times \dfrac{{m{a^2}}}{6}$
$\Rightarrow {I_{AB}} = 2 \times {I_Z}$
Since ${I_Z}$ is $20\,kg\,{m^2}$, we have,
${I_{AB}} = 2 \times 20$
$\therefore {I_{AB}} = 40\,kg - {m^2}$

So, the correct answer is option C.

Note: Students may incorrectly calculate the moment of inertia about the axis at the edge of the lamina perpendicular to the plane of the lamina. In the given question, we are asked to determine the moment of inertia about an axis touching its side and in the plane of the lamina. The crucial step in the solution is to remember the moment of inertia of the square lamina about the axis passing through its centre.