Question

The moment of inertia of a solid cylinder about its natural axis is $I$ . If its moment of inertia about an axis perpendicular to natural axis and passing through one end of cylinder is $\dfrac{{19}}{6}I$ then the ratio of radius of cylinder and its length is:
(A) $1:2$
(B) $1:3$
(C) $1:4$
(D) $2:3$

Answer 1

For solving this question, find out the moment of inertia of the cylinder about the axis perpendicular to the natural axis and passing through the center of gravity. Then apply the parallel axis theorem to find out the value of moment of inertia about the parallel axis passing through one end of the cylinder and compare it with the value given in the question.

Formula used:
The moment of inertia of a solid cylinder about its natural axis is $\dfrac{{M{R^2}}}{2}$ , and the moment of inertia of a solid cylinder about an axis perpendicular to the natural axis and passing through its center of gravity is
$\Rightarrow \dfrac{{M{R^2}}}{4} + \dfrac{{M{L^2}}}{{12}}$
Where $M =$ Mass of the cylinder, Radius of the cylinder, and $L =$ Length of the cylinder

Complete step by step answer:
We know that the moment of inertia of the solid cylinder about its natural axis is $\dfrac{{M{R^2}}}{2}$
So, moment of inertia $(I)$ about ${I_1}$ is
$\Rightarrow I = \dfrac{{M{R^2}}}{2}$ ………………..(1)
Also, the moment of inertia of a solid cylinder about the axis perpendicular to the natural axis and passing through its center of gravity is $\dfrac{{M{R^2}}}{4} + \dfrac{{M{L^2}}}{{12}}$
So, moment of inertia $(I')$ about ${I_3}$ is
$\Rightarrow I' = \dfrac{{M{R^2}}}{4} + \dfrac{{M{L^2}}}{{12}}$ ………………..(2)

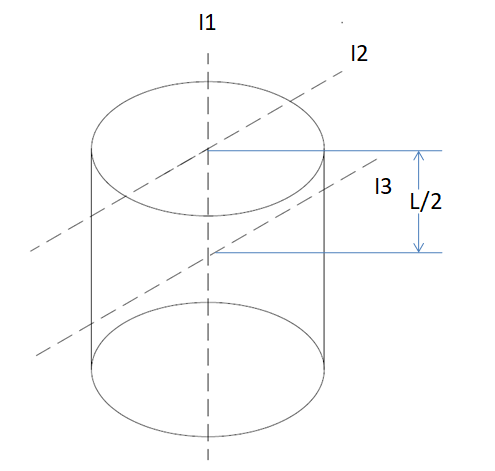
Now, ${I_2}$ is the axis perpendicular to the natural axis $({I_1})$ and passes through one end of the cylinder.
For obtaining the moment of inertia of the cylinder about the axis ${I_2}$ , we use the parallel axis theorem to shift the moment of inertia about ${I_3}$ to ${I_2}$ .
Substituting the value of $I'$ from (2), we have
$\Rightarrow I'' = \dfrac{{M{R^2}}}{4} + \dfrac{{M{L^2}}}{{12}} + M{\left( {\dfrac{L}{2}} \right)^2}$
$\Rightarrow I'' = \dfrac{{M{R^2}}}{4} + \dfrac{{M{L^2}}}{{12}} + \dfrac{{M{L^2}}}{4}$
Multiplying and dividing the last term by 3
$\Rightarrow I'' = \dfrac{{M{R^2}}}{4} + \dfrac{{M{L^2}}}{{12}} + \dfrac{{3M{L^2}}}{{12}}$
$\Rightarrow I'' = \dfrac{{M{R^2}}}{4} + \dfrac{{4M{L^2}}}{{12}}$
Finally, we have
$\Rightarrow I'' = \dfrac{{M{R^2}}}{4} + \dfrac{{M{L^2}}}{3}$
Now, according to the question,
Substituting the value of $I$ from (1)
$\Rightarrow I'' = \dfrac{{19M{R^2}}}{{12}}$ ………………..(3)
From (2) and (3), we have
$\Rightarrow \dfrac{{19M{R^2}}}{{12}} = \dfrac{{M{R^2}}}{4} + \dfrac{{M{L^2}}}{3}$
$\Rightarrow \dfrac{{19M{R^2}}}{{12}} - \dfrac{{M{R^2}}}{4} = \dfrac{{M{L^2}}}{3}$
Multiplying and dividing the second term on LHS by 3
$\Rightarrow \dfrac{{19M{R^2}}}{{12}} - \dfrac{{3M{R^2}}}{{12}} = \dfrac{{M{L^2}}}{3}$
$\Rightarrow \dfrac{{16M{R^2}}}{{12}} = \dfrac{{M{L^2}}}{3}$
Multiplying by 3 on both sides
$\Rightarrow \dfrac{{48M{R^2}}}{{12}} = M{L^2}$
$\Rightarrow 4M{R^2} = M{L^2}$
Dividing by $M$ on both the sides
$\Rightarrow 4{R^2} = {L^2}$
$\Rightarrow \dfrac{{{R^2}}}{{{L^2}}} = \dfrac{1}{4}$
Taking square root
$\Rightarrow \dfrac{R}{L} = \dfrac{1}{2}$
Hence, the correct answer is option (A), $1:2$ .

Note:
The parallel axis theorem must be carefully applied keeping in mind its statement. According to this theorem, we can shift the moment of inertia of a body about an axis passing through its center of gravity to a parallel axis. If an axis is not passing through the center of gravity, then its moment of inertia cannot be shifted.