Question

The moment of inertia of a rigid body is independent of
A. Mass of body
B. Position of axis
C. Nature of distribution of mass about axis of rotation
D. Angular velocity

Answer 1

Moment of inertia of a body is said to be the quantity that is conveyed by the body opposing the angular acceleration which is the product of the mass of every particle and square of the distance from the axis of the rotation. Hence we need to find whether it is dependent on the angular acceleration.

Complete step by step solution:
The moment of inertia is defined as the quantity which determines the amount of torque required for a definite angular acceleration within a rotational axis. It is also called the angular mass or rotational inertia. The moment of inertia of a body is governed by factors such as the density of the material, shape, and size of the body, and axis of the rotation. For equal mass and size of a solid body, the mass is distributed is determined relative to the axis. As the mass or body gets distant from the axis, the bigger is the coefficient.

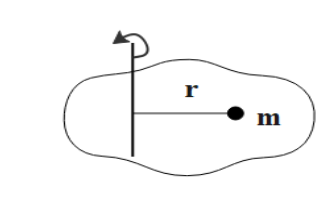
Here, we can say that the above body is a group of small point masses. Let us consider the mass of the point mass to be $m$ and its distance from the axis to be $r$ . So, the moment of inertia of the mass $m$ is can be written as,
$I = m{r^2}$
From the given options the conclusion is that the moment of inertia of a body is not dependent on the angular velocity of the body. The moment of inertia of a body is not dependent on its angular velocity. It is dependent on the position and orientation of the axis of rotation, shape and also the size of the body, and the distribution of mass of the body around the axis of rotation.
Option (D) Angular velocity is the correct answer.

Note:
If we are taking a non-rotating body then, Inertia can be explained as opposition to change in the state of motion. As the mass increases its resistance to change its motion also increases. Accordingly, we can conclude that it depends on the mass of the body.