Solveeit Logo
Login

Question

Question: The molar solubility of lead(II) azide, $Pb(N_3)_2$, in a buffer solution with pH = 1.00, is _____ $...

The molar solubility of lead(II) azide, Pb(N3)2Pb(N_3)_2, in a buffer solution with pH = 1.00, is _____ molL−1molL^{-1}. Given that

Pb(N3)2(s)⇌Pb2+(aq)+2N3−(aq);Ksp=2.5×10−9Pb(N_3)_2(s) \rightleftharpoons Pb^{2+}(aq) + 2N_3^-(aq); \qquad K_{sp} = 2.5 \times 10^{-9}

HN3(aq)+H2O(l)⇌H3O+(aq)+N3−(aq);Ka=2.0×10−5HN_3(aq) + H_2O(l) \rightleftharpoons H_3O^+(aq) + N_3^-(aq); \qquad K_a = 2.0 \times 10^{-5}

Answer

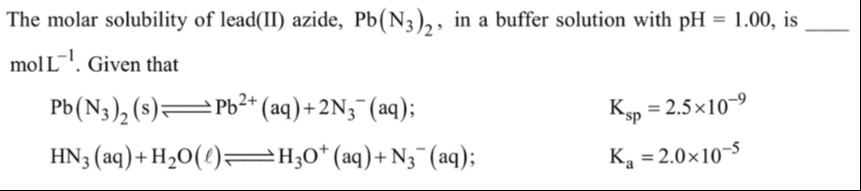
0.25

Explanation

Solution

The molar solubility of lead(II) azide, Pb(N3)2Pb(N_3)_2, in a buffer solution with pH = 1.00 needs to be calculated.

The dissolution equilibrium of Pb(N3)2Pb(N_3)_2 is: Pb(N3)2(s)⇌Pb2+(aq)+2N3−(aq)Pb(N_3)_2(s) \rightleftharpoons Pb^{2+}(aq) + 2N_3^-(aq)

The solubility product constant is Ksp=[Pb2+][N3−]2=2.5×10−9K_{sp} = [Pb^{2+}][N_3^-]^2 = 2.5 \times 10^{-9}.

Let SS be the molar solubility of Pb(N3)2Pb(N_3)_2. Then, at equilibrium, [Pb2+]=S[Pb^{2+}] = S.

The total concentration of azide species originating from the dissolution of Pb(N3)2Pb(N_3)_2 is 2S2S. These azide species can exist as N3−N_3^- or HN3HN_3 in the solution due to the acid-base equilibrium of the azide ion.

The azide ion (N3−N_3^-) is the conjugate base of the weak acid hydrazoic acid (HN3HN_3). The equilibrium is: HN3(aq)+H2O(l)⇌H3O+(aq)+N3−(aq)HN_3(aq) + H_2O(l) \rightleftharpoons H_3O^+(aq) + N_3^-(aq)

The acid dissociation constant is Ka=[H3O+][N3−][HN3]=2.0×10−5K_a = \frac{[H_3O^+][N_3^-]}{[HN_3]} = 2.0 \times 10^{-5}. Let [H+][H^+] represent [H3O+][H_3O^+].

The pH of the buffer solution is given as 1.00, so [H+]=10−pH=10−1.00=0.10 M[H^+] = 10^{-pH} = 10^{-1.00} = 0.10 \, M.

From the KaK_a expression, we can relate the concentrations of N3−N_3^- and HN3HN_3: [HN3]=[H+][N3−]Ka=0.10 M2.0×10−5[N3−]=10−12×10−5[N3−]=0.5×104[N3−]=5000[N3−][HN_3] = \frac{[H^+][N_3^-]}{K_a} = \frac{0.10 \, M}{2.0 \times 10^{-5}} [N_3^-] = \frac{10^{-1}}{2 \times 10^{-5}} [N_3^-] = 0.5 \times 10^4 [N_3^-] = 5000 [N_3^-].

The total concentration of azide species is the sum of the concentrations of N3−N_3^- and HN3HN_3: 2S=[N3−]+[HN3]2S = [N_3^-] + [HN_3]

Substitute the expression for [HN3][HN_3] in terms of [N3−][N_3^-]: 2S=[N3−]+5000[N3−]=5001[N3−]2S = [N_3^-] + 5000 [N_3^-] = 5001 [N_3^-] So, [N3−]=2S5001[N_3^-] = \frac{2S}{5001}.

Now substitute the concentrations of Pb2+Pb^{2+} and N3−N_3^- into the KspK_{sp} expression: Ksp=[Pb2+][N3−]2K_{sp} = [Pb^{2+}][N_3^-]^2 2.5×10−9=S(2S5001)22.5 \times 10^{-9} = S \left(\frac{2S}{5001}\right)^2 2.5×10−9=S4S2(5001)22.5 \times 10^{-9} = S \frac{4S^2}{(5001)^2} 2.5×10−9=4S3(5001)22.5 \times 10^{-9} = \frac{4S^3}{(5001)^2}

Solve for S3S^3: S3=2.5×10−9×(5001)24S^3 = \frac{2.5 \times 10^{-9} \times (5001)^2}{4} Calculate (5001)2(5001)^2: (5001)2=25010001(5001)^2 = 25010001 Substitute this value into the equation for S3S^3: S3=2.5×10−9×250100014S^3 = \frac{2.5 \times 10^{-9} \times 25010001}{4} S3=62525002.5×10−94S^3 = \frac{62525002.5 \times 10^{-9}}{4} S3=15631250.625×10−9S^3 = 15631250.625 \times 10^{-9} S3=0.015631250625S^3 = 0.015631250625

Now take the cube root to find SS: S=0.0156312506253S = \sqrt[3]{0.015631250625} S=0.250070015...S = 0.250070015...

Rounding to a suitable number of significant figures (given KspK_{sp} and KaK_a have 2 significant figures, and pH has 2 decimal places implying 2 significant figures for concentration), we can round to 2 significant figures. S≈0.25 molL−1S \approx 0.25 \, molL^{-1}.