Question

The modulus and amplitude of $\dfrac{1+2i}{1-(1-i)^2}$ are:
A. $\sqrt{2}$ and $\dfrac{\pi}{6}$
B. 1 and $\dfrac{\pi}{6}$
C. 1 and 0
D. 1 and $\dfrac{\pi}{3}$

Answer 1

A good way to start would be to resolve the given number into its real part and imaginary by expanding the denominator and solving it. Now, plot the real and imaginary parts as coordinates on a complex plane. Then, recall that the modulus of a complex number signifies the distance to the number from the origin of the complex plane, and that the amplitude gives the angle of inclination between the line joining the number from the origin and the x-(real) axis. Using these definitions, find its modulus and amplitude.

Formula used: Modulus of a complex number $a+ib$: $|z| = \sqrt{a^2 +b^2}$
Amplitude (argument) of a complex number $a+ib$: $\theta = tan^{-1} \left(\dfrac{b}{a}\right)$

Complete step by step answer:
A complex number is a numerical structure that can be expressed in the form of $a+ib$, where a and b are real numbers i represents an imaginary unit given by $i =\sqrt{-1}$. The $a$ part of the complex number is called the real part, whereas the $ib$ part of the complex number is called the imaginary part. Since no real number satisfies the equation $i^2=-1$, we call such numbers imaginary.
Complex numbers can be illustrated in the form of a vector diagram as coordinates on the cartesian plane called the Argand diagram. The x-axis represents the real axis and the y-axis represents the imaginary axis.
Alternatively, the coordinates of a complex number can also be visualized on the polar plane represented by the distance of the point z from the origin 0, and the angle between the positive real axis and the line segment 0z.

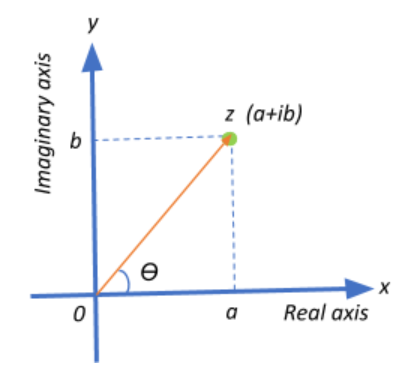
We are given a complex number of the form $\dfrac{1+2i}{1-(1-i)^2}$. In order to be able to plot them on the complex plane we need to arrive at a real part and an imaginary part of the number. For his, we just solve it:
$\dfrac{1+2i}{1-(1-i)^2} \Rightarrow \dfrac{1+2i}{1-(1+i^2-2i)}$.
Now, since $i=\sqrt{-1}$, $i^2=-1$
$\Rightarrow \dfrac{1+2i}{1-(-2i)} = \dfrac{1+2i}{1+2i} = 1 +0i$
Thus we get a complex number $1+0i$, with $a=1$ and $b=0$
Now, the modulus a complex number $a+ib$ is given as $|z| = \sqrt{a^2 +b^2}$. This represents the distance 0z, which is the absolute value of the complex number.
$\Rightarrow |z| = \sqrt{1^2 +0^2} = 1$.
Therefore, our point z is at a distance of 1 unit from the origin.
Now, the amplitude of a complex number $a+ib$ is given as $\theta = tan^{-1} \left(\dfrac{b}{a}\right)$
$\Rightarrow \theta=tan^{-1}\dfrac{0}{1} = tan^{-1}(0) = 0$.
This means that the angle between the positive x-axis and the line segment 0z is $0^{\circ}$

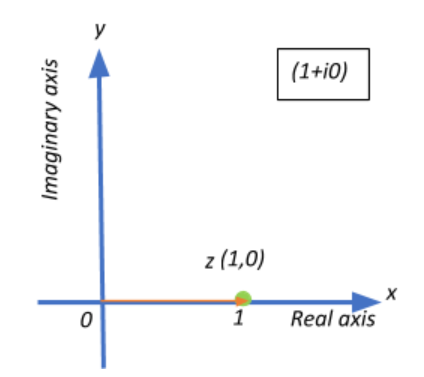
So, the correct answer is “Option C”.

Note: From our result, we obtained that the complex number is at a distance of 1 unit from the origin and is at an angle $0^{\circ}$ with the real axis.
This means that the complex number lies on the x-axis. If this is the case, then the modulus is given as $|z| = \sqrt{a^2} =|a|$. This means that the absolute value of a real number equals its absolute value as a complex number.
Similarly, if we have a complex number with only a y-coordinate, the modulus is given as $|z| = \sqrt{b^2} =|b|$. This means that the absolute value of an imaginary number equals its absolute value as a complex number.