Solveeit Logo
Login

Question

Question: The minimum value of the expression cos2x+cosx for real values of x is: [a] \(\dfrac{-9}{8}\) [b...

The minimum value of the expression cos2x+cosx for real values of x is:
[a] −98\dfrac{-9}{8}
[b] 0
[c] -2
[d] None of these

Explanation

Solution

Hint: Checking for critical points in the intervale [0,2π)[0,2\pi ) is sufficient due to periodicity of cos x and cos2x. Differentiate once w.r.t x and put derivative equal to 0 to find the critical points. Use the first derivative test to determine whether a critical point is local maxima or minima.

Complete step-by-step answer:
First derivative test: If f(x) is a continuous and differentiable function and f’(a) = 0, then
[i] If lim⁡x→a− f′(x)>0\underset{x\to {{a}^{-}}}{\mathop{\lim }}\,f'\left( x \right)>0 and lim⁡x→a+ f′(x)<0\underset{x\to {{a}^{+}}}{\mathop{\lim }}\,f'\left( x \right)<0, then x = a is a point of local maxima
[ii] If lim⁡x→a− f′(x)<0\underset{x\to {{a}^{-}}}{\mathop{\lim }}\,f'\left( x \right)<0 and lim⁡x→a+ f′(x)>0\underset{x\to {{a}^{+}}}{\mathop{\lim }}\,f'\left( x \right)>0, then x = a is a point of local minima
Let f(x) = cos2x+cosx
Differentiating once we get
f’(x) = -2sin2x-sinx = 0
i.e. 2sin2x+sinx = 0
We know that sin2x = 2sinx cosx
Using the above formula, we get
4sinxcosx+sinx = 0
Taking sinx common, we get
sinx(4cosx+1)=0
i.e sinx = 0 or 4cosx + 1 = 0
if sinx = 0 then x=0,πx=0,\pi {Because sinx = 0 when x=nπx=n\pi }
if 4cosx +1 = 0 then
cos⁡x=−14 ⇒x=π+arccos⁡(14),π−arccos⁡(14) \begin{aligned} & \cos x=\dfrac{-1}{4} \\\ & \Rightarrow x=\pi +\arccos \left( \dfrac{1}{4} \right),\pi -\arccos \left( \dfrac{1}{4} \right) \\\ \end{aligned}
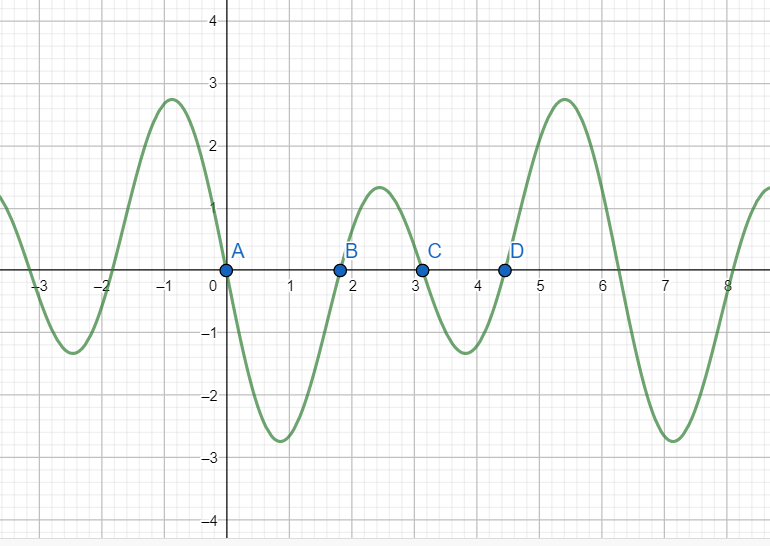
In finding the above roots, we have used the property cos⁡(arccos⁡x)=x\cos \left( \arccos x \right)=x and cos⁡(π−θ)=cos⁡(π+θ)=−cos⁡θ\cos \left( \pi -\theta \right)=\cos \left( \pi +\theta \right)=-\cos \theta .

The graph of f’(x) is shown above.
Around point x = 0(Point A in the graph of f’(x)): f’(x) changes sign from +ve to -ve as we move left of 0 to right of 0. Hence, from first derivative test, x = 0 is a point of local maxima
Around point x=π−arccos⁡(14)x=\pi -\arccos \left( \dfrac{1}{4} \right)(Point B in the graph of f’(x)): f’(x) changes sign from -ve to +ve as we move left of π−arccos⁡(14)\pi -\arccos \left( \dfrac{1}{4} \right) to the right of π−arccos⁡(14)\pi -\arccos \left( \dfrac{1}{4} \right). Hence, from the first derivative test, x=π−arccos⁡(14)x=\pi -\arccos \left( \dfrac{1}{4} \right) is a point of local minima.
Around point x=πx=\pi (Point C in the graph of f’(x)): f’(x) changes sign from +ve to -ve as we move left of π\pi to the right of π\pi .
Around point x=π+arccos⁡(14)x=\pi +\arccos \left( \dfrac{1}{4} \right) (Point D in the graph of f(x)): f’(x) changes sign from -ve to +ve as we move left of π+arccos⁡(14)\pi +\arccos \left( \dfrac{1}{4} \right) to the right of π+arccos⁡(14)\pi +\arccos \left( \dfrac{1}{4} \right). Hence x=π+arccos⁡(14)x=\pi +\arccos \left( \dfrac{1}{4} \right) is a point of local minima.
Now
f(π−arccos⁡(14))=cos⁡(2π−2arccos⁡(14))+cos⁡(π−arccos⁡(14)) =cos⁡(2arccos⁡(14))−cos⁡(arccos⁡(14)) =2cos⁡2(arccos⁡(14))−1−14 =216−54 =−98 \begin{aligned} & f\left( \pi -\arccos \left( \dfrac{1}{4} \right) \right)=\cos \left( 2\pi -2\arccos \left( \dfrac{1}{4} \right) \right)+\cos \left( \pi -\arccos \left( \dfrac{1}{4} \right) \right) \\\ & =\cos \left( 2\arccos \left( \dfrac{1}{4} \right) \right)-\cos \left( \arccos \left( \dfrac{1}{4} \right) \right) \\\ & =2{{\cos }^{2}}\left( \arccos \left( \dfrac{1}{4} \right) \right)-1-\dfrac{1}{4} \\\ & =\dfrac{2}{16}-\dfrac{5}{4} \\\ & =\dfrac{-9}{8} \\\ \end{aligned}
and
f(π+arccos⁡(14))=cos⁡(2π+2arccos⁡(14))+cos⁡(π+arccos⁡(14)) =cos⁡(2arccos⁡(14))−cos⁡(arccos⁡(14)) =2cos⁡2(arccos⁡(14))−1−14 =216−54 =−98 \begin{aligned} & f\left( \pi +\arccos \left( \dfrac{1}{4} \right) \right)=\cos \left( 2\pi +2\arccos \left( \dfrac{1}{4} \right) \right)+\cos \left( \pi +\arccos \left( \dfrac{1}{4} \right) \right) \\\ & =\cos \left( 2\arccos \left( \dfrac{1}{4} \right) \right)-\cos \left( \arccos \left( \dfrac{1}{4} \right) \right) \\\ & =2{{\cos }^{2}}\left( \arccos \left( \dfrac{1}{4} \right) \right)-1-\dfrac{1}{4} \\\ & =\dfrac{2}{16}-\dfrac{5}{4} \\\ & =\dfrac{-9}{8} \\\ \end{aligned}
Hence the minimum value of the trigonometric expression cos2x+cosx is −98\dfrac{-9}{8}.
Hence option [a] is correct.

Note: Alternative solution:
We know cos⁡2x=2cos⁡2x−1\cos 2x=2{{\cos }^{2}}x-1
Hence cos⁡2x+cos⁡x=2cos⁡2x−1+cos⁡x\cos 2x+\cos x=2{{\cos }^{2}}x-1+\cos x
Put t=cos⁡xt=\cos x we getf(t)=2t2+t−1,−1≤t≤1f\left( t \right)=2{{t}^{2}}+t-1,-1\le t\le 1
We know the quadratic expression ax2+bx+ca{{x}^{2}}+bx+c where a>0 attains minima when x=−b2ax=\dfrac{-b}{2a}
Since −b2a=−12×2=−14\dfrac{-b}{2a}=\dfrac{-1}{2\times 2}=\dfrac{-1}{4} is in the domain of t.
We have the minimum value of f(x) = minimum value of f(t)
=2(−14)2+−14−1 =18−54 =−98 \begin{aligned} & =2{{\left( \dfrac{-1}{4} \right)}^{2}}+\dfrac{-1}{4}-1 \\\ & =\dfrac{1}{8}-\dfrac{5}{4} \\\ & =\dfrac{-9}{8} \\\ \end{aligned}
which is the same as obtained above.