Question

The minimum value of the coefficient of friction between the object and floor of the truck which makes rolling of the object possible is $\mu = \dfrac{a}{{Kg}}$ . What will be K?

Answer 1

Hint
(1) In this question form equation of motion for translation and rotational motion separately and then solve these two equations to find the value of static friction by applying the condition of pure rolling motion (Given).
(2) For the body to be in rolling motion static friction must be less than and equal to kinetic friction.

Complete Step By Step Solution
Suppose F is the driving force acting by engine in the forward direction and f is the frictional force at the point of contact between floor and object. The diagram is given below-

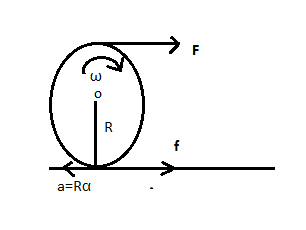
As we don’t know the direction of frictional force, you can take any of the directions forward or backward. Assume f is acting in the forward direction. So that angular velocity (ω) is clockwise direction.
Assume ‘m’ is the mass of the body.
Assume ‘a’ is the translational acceleration of the body.
Assume ‘α’ is the angular acceleration of the body.
Since the centre of mass is moving with acceleration ‘a’. So force in the translation motion is given by
$F + f = ma$ -- (1)
‘F’ and ‘f’ is the force that produces torque in the body, because of this torque angular acceleration produced in the body (angle between these forces with R is ). So torque is given by
$FR\operatorname{Sin} {90^ \circ } - fR\operatorname{Sin} {90^ \circ } = I\alpha$
Since, $\operatorname{Sin} {90^ \circ } = 1$
$FR - fR = I\alpha$ -- (2)
Moment of inertia of the truck wheel is equal to the moment of inertia of the ring because the truck wheel resembles a ring (axis of rotation passes through the centre of the ring). So moment of inertia of wheel is
$I = \dfrac{1}{2}m{R^2}$ -- (3)
Condition of rolling motion is
$a = R\alpha$
On interchanging the terms we get
$\alpha = \dfrac{a}{R}$ -- (4)
From equation (2), (3) and (4) we get
$FR - fR = \dfrac{1}{2}m{R^2}\dfrac{a}{R}$ (Torque due to force F is clockwise and frictional force f is anticlockwise)
Cancel ‘R’ from both side and from numerator and denominator we get
$F - f = \dfrac{1}{2}ma$ -- (5)
Subtract equation (5) from equation (1),
$2f = ma - \dfrac{{ma}}{2}$
On simplification we get
$f = \dfrac{{ma}}{4}$
This is the static friction value which help body to come in rolling motion
${f_{static}} = \dfrac{{ma}}{4}$ -- (6)
We know that for the rolling to be possible static friction must be less than and equal to kinetic friction.
Value of kinetic friction is given as
${f_{kinetic}} = \mu mg$ -- (7)
From equation (6) and (7)
$\dfrac{{ma}}{4} \leqslant \mu mg$
Cancel out terms from both side and on further simplification we get
$\mu \geqslant \dfrac{a}{{4g}}$
So the minimum value of the coefficient of friction between the object and floor of the truck which makes rolling of the object possible is $\mu = \dfrac{a}{{4g}}$ .
From this we get value of K,
$\Rightarrow K = 4$

Note
Similar method is used to find linear acceleration, angular acceleration, and driving force in anybody. Remember that friction is the force which is responsible for rolling motion in the body but it becomes zero when the body starts rolling.