Question

The minimum number of unequal vectors whose sum can be zero is
A. 1
B. 2
C. 3
D. 4

Answer 1

We can approach this question in a step by step manner. That means we will consider the possibility of sum of a single vector, sum of two vectors (same magnitude but different direction) and also the sum of three vectors being zero. And then we find the possibility that directly satisfies the condition given in the question.

Complete step-by-step answer:
We see that, in this question we are asked to find the minimum number of ‘unequal vectors’ whose sum can be zero.
Let us consider zero vectors (As there is no mention of ‘non-zero’ vectors). We know that Zero vectors are vectors with zero magnitude and an arbitrary direction. Examples of zero vectors are position vector of origin of the coordinate axes, velocity vector of a stationary body, etc. Sum of a zero vector cannot be considered as we don’t consider the sum of a single vector a proper sum.
The answer now depends on your meaning of ‘unequal’. We could consider two vectors of equal magnitude but different directions unequal vectors.

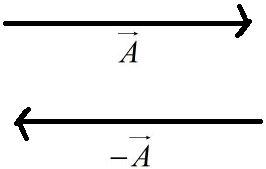
Here,
$\overrightarrow{A}+(-\overrightarrow{A})=\overrightarrow{A}-\overrightarrow{A}=0$
$\Rightarrow \overrightarrow{A}\ne -\overrightarrow{A}$
But,
$\left| \overrightarrow{A} \right|=\left| -\overrightarrow{A} \right|$
Here, we could say that the sum of two unequal vectors with the same magnitude but different direction gives you zero.
But let us assume that, in this question by ‘unequal vectors’ it is meant unequal by all sense, that is, both by magnitude and direction.
Let us take three unequal vectors
$\Rightarrow \overrightarrow{A}$, $\overrightarrow{B}$ and $\overrightarrow{C}$
Such that,
$\overrightarrow{A}\ne \overrightarrow{B}\ne \overrightarrow{C}$
But,
$\overrightarrow{C}=-\left( \overrightarrow{A}+\overrightarrow{B} \right)$
So by adding the 3 vectors we get the sum as,
$\overrightarrow{A}+\overrightarrow{B}+\overrightarrow{C}=\overrightarrow{A}+\overrightarrow{B}+\left( -\left( \overrightarrow{A}+\overrightarrow{B} \right) \right)$
$\Rightarrow \overrightarrow{A}+\overrightarrow{B}+\overrightarrow{C}=\left( \overrightarrow{A}-\overrightarrow{A} \right)+\left( \overrightarrow{B}-\overrightarrow{B} \right)$
$\Rightarrow \overrightarrow{A}+\overrightarrow{B}+\overrightarrow{C}=0$
Since this question lacks specifications about the meaning of the word ‘unequal’, we have to consider the case of perfectly unequal vectors, that is, unequal both magnitude as well as direction. In that case the minimum number of unequal vectors whose sum can be zero is 3.

So, the correct answer is “Option C”.

Note: While dealing with any conceptual MCQs, we should consider the possibility of each option being the answer. Here, in this question we have seen that a simple specification results in entirely different answers. So, make sure that you focus on these specifications.