Question

The minimum magnetic dipole moment of an electron in the hydrogen atom is

A) $\dfrac{{eh}}{{2\pi m}}$
B) $\dfrac{{eh}}{{4\pi m}}$
C) $\dfrac{{eh}}{{\pi m}}$
D) $0$

Answer 1

The electron revolving around the nucleus in an orbit of radius $r$ generates a current $i$ and a current carrying loop produces a magnetic dipole moment.

Formula Used:
1. Current $i$ generated by the revolving electron is given by, $i = \dfrac{e}{T}$ where $e$ is the charge of the electron and $T = \dfrac{{2\pi }}{\omega }$ is the time period ($\omega$is the angular velocity).
2. Relation between linear velocity $v$ and angular velocity$\omega$ with $r$ as the radius is given by,

$v = r\omega$ or $\omega = \dfrac{v}{r}$ .

3. Magnetic dipole moment is $\mu = iA$ ,where $i$ is the current flowing through a loop of area $A$ .
Angular momentum of an electron of mass $m$ moving with a velocity $v$along a circular orbit of radius $r$ is $L = mvr$ .
4. From Bohr’s postulate we have, $mvr = \dfrac{{nh}}{{2\pi }}$ , $n$ is the principal quantum number and $h$ is the Planck's constant.

Complete step by step answer:
Step1: Sketch a schematic diagram of the electron in the hydrogen atom.

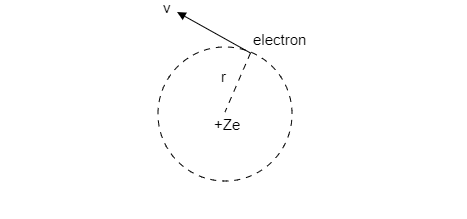
Step 2: Express the relation for the current generated by the revolving electron.

The electron revolving around the nucleus of the hydrogen atom is like the current flowing through a current carrying loop that encompasses an area $A$.

So, the current generated by an electron of charge $e$ revolving around the orbit of radius $r$for a time $T$with angular velocity $\omega$ is given by, $i = \dfrac{e}{T}$ .

 Substitute $T = \dfrac{{2\pi }}{\omega }$ in the above equation to get, $i = \dfrac{{e\omega }}{{2\pi }}$ .  

Substituting for $\omega = \dfrac{v}{r}$ in the equation for current, we get $i = \dfrac{{ev}}{{2\pi r}}$ .

Step 3: Express the relation for magnetic dipole moment of the electron in the hydrogen atom.
Magnetic dipole moment $\mu$ of a current carrying loop of area $A$ is given by, $\mu = iA$ .

The area of the orbit (or loop) along which the electron revolves is given by, $A = \pi {r^2}$as we assume the orbit to be circular.

Now substitute for $i = \dfrac{{ev}}{{2\pi r}}$ and $A = \pi {r^2}$ to obtain the magnetic dipole moment $\mu$ .

We have, $\mu = \left( {\dfrac{{ev}}{{2\pi r}}} \right)\pi {r^2}$ .

Simplifying we get,$\mu = \dfrac{{evr}}{2}$ .

Step 4: Express the magnetic dipole moment $\mu$ in terms of the angular momentum $L = mvr$ .

Angular momentum of a mass $m$ moving with a velocity $v$along a circular orbit of radius $r$ is $L = mvr$ .

i.e., $vr = \dfrac{L}{m}$ .

Substituting the above relation in the equation $\mu$ we get, $\mu = \dfrac{e}{{2m}}L$ .

Step 5: Use Bohr’s postulate about angular momentum to obtain the minimum magnetic dipole moment of the electron in the hydrogen atom.

According to Bohr’s atomic model, the angular momentum of the electron orbiting around the nucleus is quantized. The angular momentum of an electron is given by,

$L = mvr = \dfrac{{nh}}{{2\pi }}$ .

Substitute $L = \dfrac{{nh}}{{2\pi }}$ in the equation $\mu = \dfrac{e}{{2m}}L$ to obtain,

$\mu = \dfrac{e}{{2m}}\left( {\dfrac{{nh}}{{2\pi }}} \right) = \dfrac{{neh}}{{4\pi m}}$ .

For minimum magnetic dipole moment, $n = 1$ ,i.e., $\mu = \dfrac{{eh}}{{4\pi m}}$ .

Therefore, the correct option is b) $\dfrac{{eh}}{{4\pi m}}$ .

Note: : It is important to evaluate the options in which quantities the final answer is expressed and hence then manipulate equations to reach to the final answer in the quantities displayed in the option.