Question

The minimum force required to move the body up an inclined plane is three times the minimum force required to prevent it from sliding down the plane. If the coefficient of friction between the body and the inclined plane is $\dfrac{1}{{2\sqrt 3 }},$ the angle of the inclined plane is
(A) $60^\circ$
(B) $45^\circ$
(C) $30^\circ$
(D) $15^\circ$

Answer 1

- We should know friction.
- We should have knowledge of all the forces acting or a body or air inclined plane.
- We need to know the relation between the frictional force $\left( {fs} \right)$ with normal reaction (R) i.e. ${f_s} = \mu R$

Complete step by step Solution:

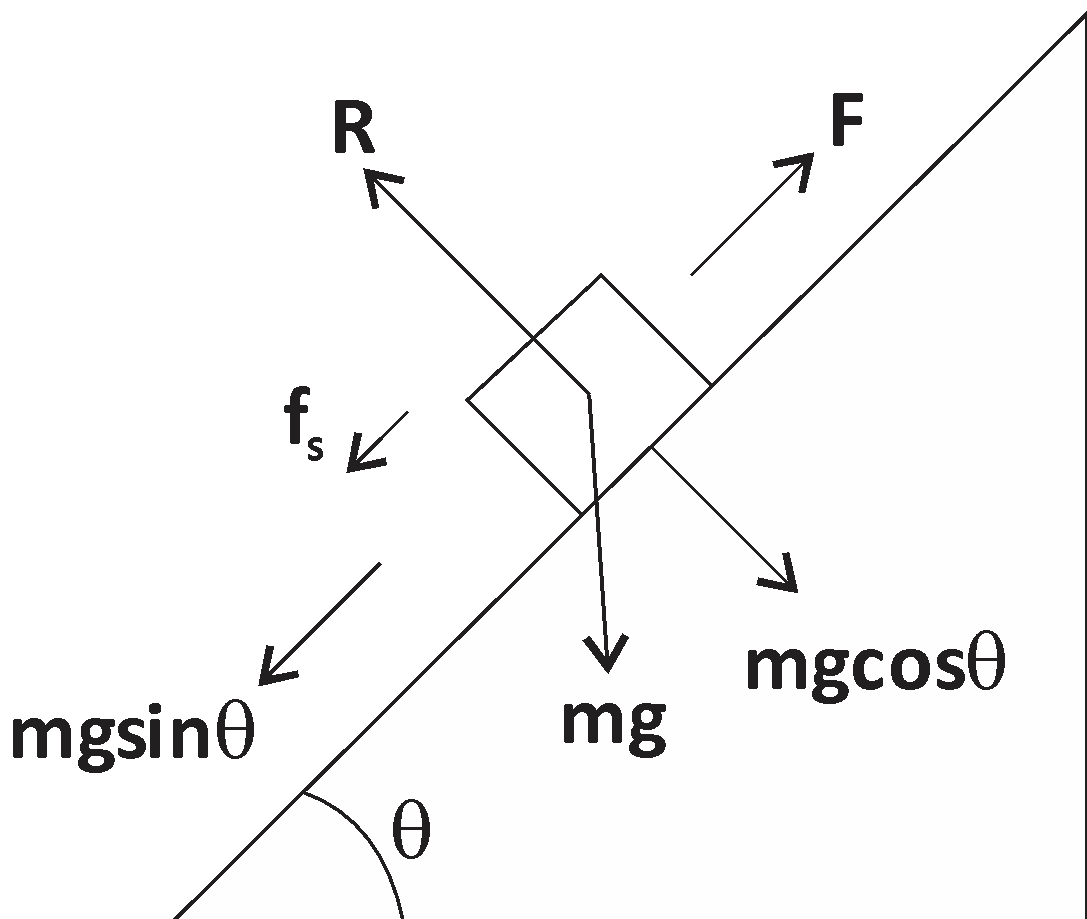
Here, the mass of the body $= {\text{ }}m$
Applied force $= {\text{ }}F,$ normal reaction $= {\text{ }}R$
Friction force $= {\text{ }}{f_s}$
Acceleration due to gravity $= {\text{ }}g$
Angle of the inclined plane $= \theta$
Coefficient of friction $=$is
Now, for the body to move up, opposing forces are $mg\sin \theta \,\,4\,\,{f_s},$ so, ${F_{up}} = mg\sin \theta + {f_s}$
${F_{up}} = mg\sin \theta + \mu R = mg\sin \theta + \mu mg\cos \theta$
For preventing the body opposing force is $mg\sin \theta$ & helping
Force ${f_s}$, so, ${F_{down}} = mg\sin \theta - \mu mg\cos \theta$
Now, given, ${F_{up}} = 3\,\,{F_{down}}$
$\Rightarrow \left( {mg\sin \theta + \mu mg\cos \theta } \right) = 3\left( {mg\sin \theta - \mu \cos \theta } \right)$
$\Rightarrow 2\sin \theta = 4\mu \,\,\cos \theta$
$\Rightarrow \tan \theta = 2\mu$
$\theta = {\tan ^ - }\left( {2\mu } \right)$
Given, $\mu = \dfrac{1}{{2\sqrt 3 }}$
$\therefore \,\,\,\theta = {\tan ^ - }\left( {\dfrac{1}{{\sqrt 3 }}} \right)$
$= 30^\circ$
So, option (c) is correct.

Note:
- We to take case while calculating upward 4 downward force
- Fup should be greater than ${F_{down}}$.
- We have to take care while calculating numerical value.