Question

The minimum distance of the center of the ellipse $\dfrac{{{x}^{2}}}{16}+\dfrac{{{y}^{2}}}{9}=1$ from the chord of contact of mutually perpendicular tangents of the ellipse is
(A) $\dfrac{144}{5}$
(B) $\dfrac{16}{5}$
(C) $\dfrac{9}{5}$
(D) None of these

Answer 1

he equation of the ellipse is, $\dfrac{{{x}^{2}}}{16}+\dfrac{{{y}^{2}}}{9}=1$ . We know the general equation of an ellipse, $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ . Now, compare $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ and $\dfrac{{{x}^{2}}}{16}+\dfrac{{{y}^{2}}}{9}=1$ , and get the value of ${{a}^{2}}$ and ${{b}^{2}}$ . We know that the perpendicular tangents meet at a point on the director circle. We know the equation of the director circle, ${{x}^{2}}+{{y}^{2}}=\sqrt{{{a}^{2}}+{{b}^{2}}}$ . Now, get the equation of the director circle. The coordinates of the general point on the director circle $\left( 5\cos \theta ,5\sin \theta \right)$ . We know the standard equation of chord of contact with respect to $\left( {{x}_{1}},{{y}_{1}} \right)$ of ellipse is, $\dfrac{x{{x}_{1}}}{{{a}^{2}}}+\dfrac{y{{y}_{1}}}{{{b}^{2}}}=1$ . Use this and get the equation of the chord of the contact with respect to the point $\left( 5\cos \theta ,5\sin \theta \right)$ . The center of the ellipse is $\left( 0,0 \right)$ and the chord of the contact $\dfrac{x\left( 5\cos \theta \right)}{16}+\dfrac{y\left( 5\sin \theta \right)}{9}-1=0$ . We know the formula of the distance of the point $\left( {{x}_{1}},{{y}_{1}} \right)$ from the equation of the line $ax+by+c$ , $\text{Distance}=\dfrac{\left| a{{x}_{1}}+b{{y}_{1}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$ . Use this formula and get the distance of the center of the ellipse and the chord of the contact. Now, put ${{\cos }^{2}}\theta =0$ and get the minimum value of the distance.

Complete step-by-step solution:
According to the question, it is given that we have an ellipse, $\dfrac{{{x}^{2}}}{16}+\dfrac{{{y}^{2}}}{9}=1$ and we have to find the minimum distance of the center of the ellipse $\dfrac{{{x}^{2}}}{16}+\dfrac{{{y}^{2}}}{9}=1$ from the chord of contact of mutually perpendicular tangents of the ellipse.
The equation of the ellipse = $\dfrac{{{x}^{2}}}{16}+\dfrac{{{y}^{2}}}{9}=1$ ……………….(1)
The center of the ellipse $\dfrac{{{x}^{2}}}{16}+\dfrac{{{y}^{2}}}{9}=1$ is at the origin.
The coordinates of the center of the ellipse = $\left( 0,0 \right)$ ………......…………….(2)
The perpendicular tangents of the ellipse meet at the point which lies on the director circle.

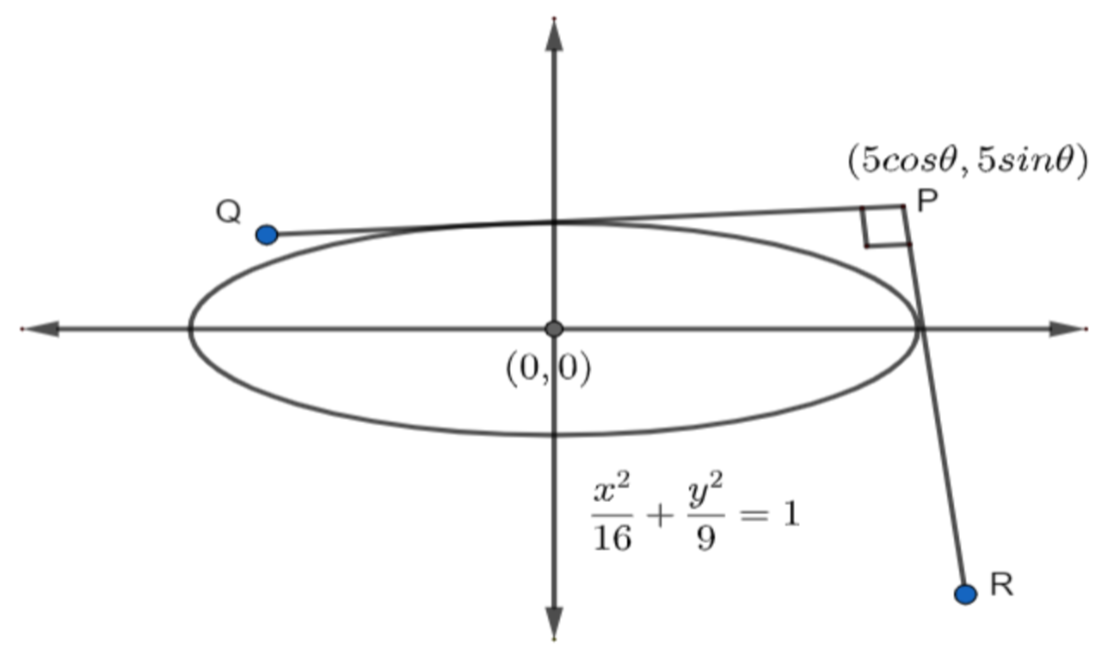
We know the standard equation of an ellipse, $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ ……………………………………..(3)
On comparing equation (1) and equation (3), we get
${{a}^{2}}=16$ ……………………………………………(4)
${{b}^{2}}=9$ ……………………………………………(5)
We know that the perpendicular tangents meet at the point on the director circle,
The standard equation of the director circle,
${{x}^{2}}+{{y}^{2}}=\sqrt{{{a}^{2}}+{{b}^{2}}}$ ………………………………………….(6)
Now, from equation (4), equation (5), and equation (6), we get

& \Rightarrow {{x}^{2}}+{{y}^{2}}=\sqrt{16+9} \\\ & \Rightarrow {{x}^{2}}+{{y}^{2}}=\sqrt{25} \\\ \end{aligned}$$ $$\Rightarrow {{x}^{2}}+{{y}^{2}}=5$$ …………………………………..……(7) The coordinates of the general point on the director circle $$\left( 5\cos \theta, 5\sin \theta \right)$$ ………………………………………(8) We know the standard equation of chord of contact with respect to $$\left( {{x}_{1}},{{y}_{1}} \right)$$ of ellipse is, $$\dfrac{x{{x}_{1}}}{{{a}^{2}}}+\dfrac{y{{y}_{1}}}{{{b}^{2}}}=1$$ …………………………………………..(9) From equation (1), equation (8), and equation (9), we get $$\Rightarrow \dfrac{x\left( 5\cos \theta \right)}{16}+\dfrac{y\left( 5\sin \theta \right)}{9}=1$$ $$\Rightarrow \dfrac{x\left( 5\cos \theta \right)}{16}+\dfrac{y\left( 5\sin \theta \right)}{9}-1=0$$ …………………………………………(10) We know the formula of the distance of the point $$\left( {{x}_{1}},{{y}_{1}} \right)$$ from the equation of the line $$ax+by+c$$ , $$\text{Distance}=\dfrac{\left| a{{x}_{1}}+b{{y}_{1}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$$ ………………………………………….(11) From equation (2), we have the coordinates of the center. Using the formula shown in equation (11) to get the distance of the center of the ellipse from the line $$\dfrac{x\left( 5\cos \theta \right)}{16}+\dfrac{y\left( 5\sin \theta \right)}{9}-1=0$$ . Now, from equation (2), equation (10), and equation (11), we get The distance of the point $$\left( 0,0 \right)$$ from the equation of the chord of contact $$\dfrac{x\left( 5\cos \theta \right)}{16}+\dfrac{y\left( 5\sin \theta \right)}{9}-1=0$$, Distance $$=\dfrac{\left| \left( \dfrac{0\left( 5\cos \theta \right)}{16}+\dfrac{0\left( 5\sin \theta \right)}{9}-1 \right) \right|}{\sqrt{{{\left( \dfrac{5\cos \theta }{16} \right)}^{2}}+{{\left( \dfrac{5\sin \theta }{9} \right)}^{2}}}}$$ $$=\dfrac{\left| \left( -1 \right) \right|}{\sqrt{{{\left( \dfrac{5\cos \theta }{16} \right)}^{2}}+{{\left( \dfrac{5\sin \theta }{9} \right)}^{2}}}}$$ $$=\dfrac{1}{\sqrt{\dfrac{25{{\cos }^{2}}\theta }{256}+\dfrac{25{{\sin }^{2}}\theta }{81}}}$$ ……………………………………………..(12) We know the identity, $${{\cos }^{2}}\theta +{{\sin }^{2}}\theta =1$$ ……………………………………………(13) Now, simplifying equation (13), we get $$\Rightarrow {{\cos }^{2}}\theta +{{\sin }^{2}}\theta =1$$ $$\Rightarrow {{\sin }^{2}}\theta =1-{{\cos }^{2}}\theta $$ ………………………………………(14) From equation (12) and equation (14), we get Distance $$=\dfrac{1}{\sqrt{\dfrac{25{{\cos }^{2}}\theta }{256}+\dfrac{25\left( 1-{{\cos }^{2}}\theta \right)}{81}}}$$ Distance $$=\dfrac{1}{\sqrt{\dfrac{25{{\cos }^{2}}\theta }{256}+\dfrac{25}{81}-\dfrac{25{{\cos }^{2}}\theta }{81}}}$$ Distance $$=\dfrac{1}{\sqrt{{{\cos }^{2}}\theta \left( \dfrac{25}{256}-\dfrac{25}{81} \right)+\dfrac{25}{81}}}$$ …………………………………………....(15) The general distance of the center of the ellipse from the chord of contact of mutually perpendicular tangents of the ellipse = $$\dfrac{1}{\sqrt{{{\cos }^{2}}\theta \left( \dfrac{25}{256}-\dfrac{25}{81} \right)+\dfrac{25}{81}}}$$ …………………………………………(16) We have to find the minimum distance of the center of the ellipse $$\dfrac{{{x}^{2}}}{16}+\dfrac{{{y}^{2}}}{9}=1$$ from the chord of contact of mutually perpendicular tangents of the ellipse. It means that when the denominator of $$\dfrac{1}{\sqrt{{{\cos }^{2}}\theta \left( \dfrac{25}{256}-\dfrac{25}{81} \right)+\dfrac{25}{81}}}$$ is maximum then the distance will be minimum And the denominator will be maximum when $${{\cos }^{2}}\theta $$ is equal to 0. Now, on putting $${{\cos }^{2}}\theta =0$$ in equation (16), we get The general distance of the center of the ellipse from the chord of contact of mutually perpendicular tangents of the ellipse, $$\begin{aligned} & =\dfrac{1}{\sqrt{0\left( \dfrac{25}{256}-\dfrac{25}{81} \right)+\dfrac{25}{81}}} \\\ & =\dfrac{1}{\sqrt{\dfrac{25}{81}}} \\\ & =\dfrac{9}{5} \\\ \end{aligned}$$ Therefore, the general distance of the center of the ellipse from the chord of contact of mutually perpendicular tangents of the ellipse is $$\dfrac{9}{5}$$ . **Hence the correct option is (C).** **Note:** In this question, one might do a silly mistake while figuring out the minimum value of $$\dfrac{1}{\sqrt{{{\cos }^{2}}\theta \left( \dfrac{25}{256}-\dfrac{25}{81} \right)+\dfrac{25}{81}}}$$ . Here, one might think that by putting $${{\cos }^{2}}\theta =1$$ in $$\dfrac{1}{\sqrt{{{\cos }^{2}}\theta \left( \dfrac{25}{256}-\dfrac{25}{81} \right)+\dfrac{25}{81}}}$$ , we can get its minimum value. This is wrong because putting the value of $${{\cos }^{2}}\theta $$ equal to 1 will not give the minimum value of $$\dfrac{1}{\sqrt{{{\cos }^{2}}\theta \left( \dfrac{25}{256}-\dfrac{25}{81} \right)+\dfrac{25}{81}}}$$ . In the denominator we have the term $${{\cos }^{2}}\theta \left( \dfrac{25}{256}-\dfrac{25}{81} \right)$$ which is negative. So, to make the denominator maximum we must reduce the negative term. So, on putting $${{\cos }^{2}}\theta =0$$ , we get the negative term equal to zero which makes the denominator to reach its maximum value.