Question

The minimum deviation produced by a hollow prism filled with certain liquid to be ${30^0}$ . The light ray is also found to be refracted at angle ${30^0}$ . The refractive index of the liquid is:
(A) $\sqrt 2$
(B) $\sqrt 3$
(C) $\sqrt {\dfrac{3}{2}}$
(D) $\dfrac{3}{2}$

Answer 1

Hint : Here, the prism given in the question is filled with the liquid with some refractive index that we have to calculate. First of all we have to find out the minimum deviation and the angle of the prism to calculate the required refractive index of the liquid inside the prism.
$\dfrac{{\sin \left( {\dfrac{{A + {\delta _m}}}{2}} \right)}}{{\sin \left( {\dfrac{A}{2}} \right)}} = \mu$

Complete Step By Step Answer:
Let minimum angle of deviation be ${\delta _m}$ , $A$ be the angle of the prism, and $\mu$ be the refractive index of the liquid in the prism, $i$ , ${r_1}$ , ${r_2}$ are the angle of incidence, refraction, refraction, respectively. Let us consider the below figure of prism.

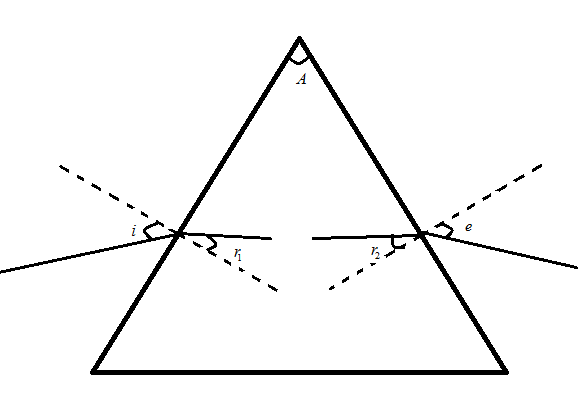
For prism in the above figure, minimum deviation is given by ${\delta _m}$
We know the condition of minimum deviation as ${r_1} = {r_2} = {30^0}$
$\therefore {\delta _m} = {30^0}$ …. $(1)$
Also, in the prism for angle of prism we have
$A = {r_1} + {r_2}$
$\Rightarrow A = {60^0}$ …. $(2)$
The refractive index of the liquid in the prism is calculated by using the formula given below,
$\dfrac{{\sin \left( {\dfrac{{A + {\delta _m}}}{2}} \right)}}{{\sin \left( {\dfrac{A}{2}} \right)}} = \mu$
By placing the values from equations $(1)$ and $(2)$
$\Rightarrow \dfrac{{\sin \left( {\dfrac{{60 + 30}}{2}} \right)}}{{\sin \left( {\dfrac{{60}}{2}} \right)}} = \mu$
$\Rightarrow \dfrac{{\sin {{45}^0}}}{{\sin {{30}^0}}} = \mu$
On solving the above equation, we get
$\therefore \mu = \sqrt 2$
The refractive index of the liquid inside the prism is $\sqrt 2$
Thus, the correct answer is the option A.

Note :
Here, it is important to have all the knowledge about the angle of deviation and also its conditions. Then use that condition to find minimum deviation and also the refractive index of the liquid. The formula we used above is very useful in every prism problem, one must learn the use of this formula.