Question

The minimum area of a triangle formed by any tangent to the ellipse $\dfrac{{{x^2}}}{{16}} + \dfrac{{{y^2}}}{{81}} = 1$ and the coordinate axes is
A. $12$
B.$18$
C.$26$
D.$36$

Answer 1

We will draw the ellipse $\dfrac{{{x^2}}}{{16}} + \dfrac{{{y^2}}}{{81}} = 1$ and draw tangent to the ellipse which cuts the positive x-axis and y-axis. Using the parametric form of point on tangent of the ellipse we substitute the values of point in the ellipse and solve the equation which becomes an equation of line in intercept form from which we get our x and y intercepts. From there we get sides of the triangle and substitute in the area of the triangle.

Formula used:
a) General equation of ellipse is given by $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$
b) General point on the ellipse in parametric form is $(a\cos \theta ,b\sin \theta )$
c) Area of a triangle is given by half the product of base and height.

Complete step-by-step answer:
We have equation of ellipse $\dfrac{{{x^2}}}{{16}} + \dfrac{{{y^2}}}{{81}} = 1$, On comparing with general equation of ellipse $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$, we get the value of ${a^2} = 16 \Rightarrow a \pm 4$ and ${b^2} = 81 \Rightarrow b = \pm 9$
We draw an ellipse and tangent to the ellipse.

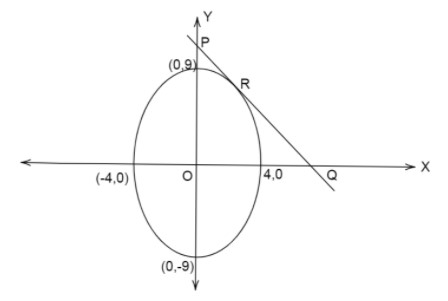
We know a point on the tangent in parametric form is $(a\cos \theta ,b\sin \theta )$
Put the value of $a = 4,b = 9$ as the point is in the first quadrant where both x and y are positive.
The point is $R(4\cos \theta ,9\sin \theta )$.
The general equation of tangent is given by $\dfrac{{x\cos \theta }}{a} + \dfrac{{y\sin \theta }}{b} = 1$
Substituting the values of a and b we get
$\dfrac{{x\cos \theta }}{4} + \dfrac{{y\sin \theta }}{9} = 1$
We can write this equation in the form
$\dfrac{x}{{\dfrac{4}{{\cos \theta }}}} + \dfrac{y}{{\dfrac{9}{{\sin \theta }}}} = 1$
Which is equation of a line in intercept form i.e. $\dfrac{x}{a} + \dfrac{y}{b} = 1$, where the x-intercept is a and y intercept is b.
So, here x intercept is $\dfrac{4}{{\cos \theta }}$ and y intercept is $\dfrac{9}{{\sin \theta }}$.
So, we can write the points on the coordinate axes as $P(0,\dfrac{9}{{\sin \theta }}),Q(\dfrac{4}{{\cos \theta }},0)$
Therefore in $\vartriangle POQ$, three vertices are $P(0,\dfrac{9}{{\sin \theta }}),Q(\dfrac{4}{{\cos \theta }},0),O(0,0)$
Area of \vartriangle POQ$$$$ = \dfrac{1}{2} \times base $\times$ height
Here base is $OQ = \dfrac{4}{{\cos \theta }}$ and height is $OP = \dfrac{9}{{\sin \theta }}$
So, Area of \vartriangle POQ$$$$ = \dfrac{1}{2} \times OQ \times OP
$$
= \dfrac{1}{2} \times \dfrac{4}{{\cos \theta }} \times \dfrac{9}{{\sin \theta }} \\
= \dfrac{{36}}{{2\cos \theta \cos \theta }} \\

Since, we know $$2\sin \theta \cos \theta = \sin 2\theta $$ Therefore, Area of $$\vartriangle POQ = \dfrac{{36}}{{\sin 2\theta }}$$ Now we have to find the minimum area of the triangle, which means we maximize the denominator on RHS of the equation So, maximum value of $$\sin 2\theta = 1$$(as sin and cos vary from -1 to 1) Therefore minimum value of area of $$\vartriangle POQ = 36$$ **So, the correct answer is “Option D”.** **Note:** Students many times substitute the point on tangent in the equation of the ellipse which will give us an equation in square of trigonometric terms which will be more difficult to solve, keep in mind that we can use general forms of equation of tangent to find the equation.In general the minimum area of the triangle formed by any tangent to the ellipse $$\dfrac{{{x^2}}}{{a}^2} + \dfrac{{{y^2}}}{{b}^2} = 1$$ with the coordinate axis is given by $ab$.