Question

The midpoint P of the line segment joining the points A (-10, 4) and B (-2, 0) lies on the line segment joining the points C (-9, -4) and D (-4, y). Find the ratio in which P divides CD and also, find the value of y.

Answer 1

Hint: Find the coordinates of the midpoint P of the line segment AB. Then use the section formula of line segment CD for the abscissa of point P to find the ratio in which P divides CD. Use the section formula of line segment CD for the ordinate of point P to find y.

Complete step-by-step answer:

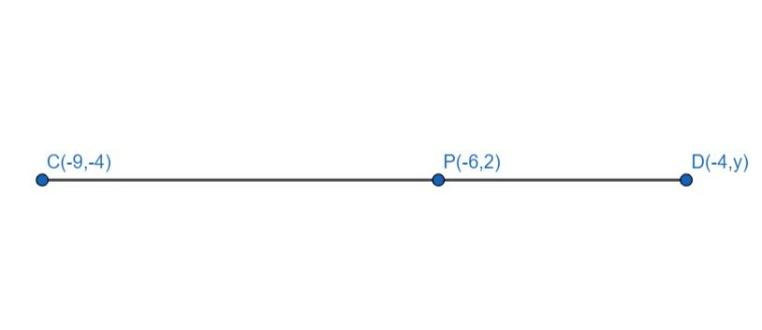
From section formula, if P (x, y) divides the line segment joining $C({x_3},{y_3})$ and $D({x_4},{y_4})$ in the ratio m:n, then:
$x = \dfrac{{m{x_4} + n{x_3}}}{{m + n}};{\text{ }}y = \dfrac{{m{y_4} + n{y_3}}}{{m + n}}{\text{ }}.........{\text{(2)}}$
Substituting equation (1) in equation (2) and using coordinates of C and D, we get:
$- 6 = \dfrac{{m( - 4) + n( - 9)}}{{m + n}}{\text{ }}..........{\text{(3)}}$
$2 = \dfrac{{m(y) + n( - 4)}}{{m + n}}{\text{ }}...........{\text{(4)}}$
Simplifying equation (3) to get the ratio in which P divided CD, we get:
$- 6 = \dfrac{{ - 4m - 9n}}{{m + n}}{\text{ }}$
$- 6(m + n) = - 4m - 9n$
$- 6m - 6n = - 4m - 9n$
$- 6m + 4m = - 9n + 6n$
$- 2m = - 3n$
$\dfrac{m}{n}{\text{ = }}\dfrac{3}{2}{\text{ }}..........{\text{(5)}}$
Simplifying equation (4) to obtain the value of y, we get:
$2 = \dfrac{{my - 4n}}{{m + n}}$
$2(m + n) = my - 4n$
$2m + 2n = my - 4n$
Gathering terms containing m on RHS and terms containing n on LHS, we get:
$4n + 2n = my - 2m$
$6n = m(y - 2)$
Divide both sides by n, to get:
$6 = \dfrac{m}{n}(y - 2)$
Substituting equation (5) in the above equation, we get:
$6 = \dfrac{3}{2}(y - 2)$
Multiply both sides by $\dfrac{2}{3}$ and simplify.
$\dfrac{2}{3} \times 6 = y - 2$
$4 = y - 2$
$y = 6$
Hence, the value of y is 6
Therefore, P divides CD in the ratio 3:2 and the value of y is 6.

Note: The possibility for mistake is writing the section formula for points $C({x_3},{y_3})$ and $D({x_4},{y_4})$ wrongly as $x = \dfrac{{m{x_3} + n{x_4}}}{{m + n}};{\text{ }}y = \dfrac{{m{y_3} + n{y_4}}}{{m + n}}$ instead of $x = \dfrac{{m{x_4} + n{x_3}}}{{m + n}};{\text{ }}y = \dfrac{{m{y_4} + n{y_3}}}{{m + n}}$ . You might also think, it is impossible to find three variables from two equations but you are just finding the ratio between m and n and then the value of y, which requires only two equations.