Question
Question: The mid-point of the line joining the points \(\left( { - 10.8} \right){\text{ and }}\left( { - 6,12...
The mid-point of the line joining the points (−10.8) and (−6,12) divides the line joining the points (4,−2) and (−2,4) in the ratio:
(1)1:2 internally
(2)1:2 externally
(3)2:1 internally
(4)2:1 externally
(5)2:3 externally
Solution
We must be familiar with the concept of section formula for internal and external division for a segment in order to solve this question. The section formula helps us to find the co-ordinates of the point dividing the segment if the section ratio in which the point divides the given line segment is known. The section formula is of two types and these types depend on the point which divides the line segment means it can be present internally or externally. We must also know how to write the equation of a line segment via the point slope form. In order to solve this question we will proceed with first finding the equation for both line segments, then we will use these equations to find the co-ordinates of the mid-point and then with the help of section formula we will find the section ratio which has been asked in this question.
Complete step by step answer:
(1) Section formula for internal division:
If C is the point which divides the line segment AB internally (means the point c is present on the line segment) in the ratio m:n , then the co-ordinates of point C are given by;
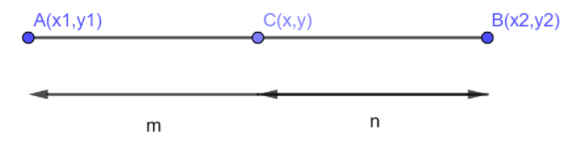
⇒C(x,y)=(m+nmx2+nx1,m+nmy2+ny1)
(2) Section formula for external division:
If C is the point which divides the line segment AB externally (means the point c lies outside the line segment) in the ratio m:n , then the co-ordinates of point C are given by;

⇒C(x,y)=(m−nmx2−nx1,m−nmy2−ny1)
Now, according to the question let us draw the scenario given to us;
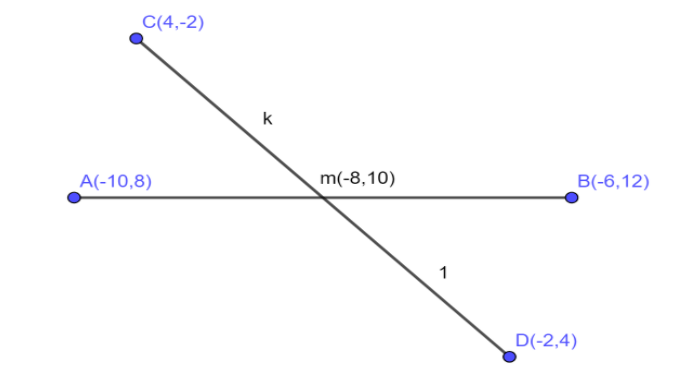
Firstly, we will find the equation of the line AB by the point slope form of equations;
⇒y−y1=x2−x1y2−y1(x−x1)
The line segment (AB) has points (−10,8) and (−6,12) as (x1,y1) and (x2,y2) respectively;
∴y−8=−6+1012−8(x+10)
Further simplifying the above equation,
⇒y−8=x+10
Therefore we get the equation of the line segment AB as;
⇒x−y+18=0 ......(1)
Now, we will find the equation of the line CD by the point slope form of equations;
The line segment (CD) has points (4,−2) and (−2,4) as (x1,y1) and (x2,y2) respectively;
∴y+2=−2−44+2(x−4)
Further simplifying the above equation,
⇒y+2=−x+4
Therefore we get the equation of the line segment CD as;
⇒x+y−2=0 ......(2)
Solving equation (1) and equation (2) to find the values of x and y ;
Adding equations (1) and equation (2) , we get;
⇒x−y+18+x+y−2=0
⇒2x+16=0
∴x=−8
Put the Value of x in equation (2) , we get;
⇒−8+y−2=0
∴y=10
Since we have the value of mid-point (x,y)=(−8,10) , now we can use the section formula to find out the section ratio;
So, let (−8,10) divide the joining of (4,−2) and (−2,4) in the ratio k : 1 ;
Using section formula we have ;
⇒−8=k+1−2k+4 ......(3)
And also, 10=k+14k−2 ......(4)
Using any of the above equation, we can find the value of k ;
Using equation (3) , we have;
⇒−8k−8=−2k+4
⇒−6k=12
Therefore, k=−2 .
Here, the value of k is negative which means that this is a case of external division .
Therefore, the correct answer for this question is option (4) , i.e. 2:1 externally.

Note: Significance of negative section ratio: The negative ratio tells us that the point dividing the line segment CD i.e. m , actually lies outside the line segment means this is a case of external division. We can also notice this via the given points of the line segment CD , the given points are (4,−2) and (−2,4) and we have calculated the co-ordinates of the point m(x,y)=(−8,10) , therefore the point m definitely lies outside the line segment CD. Figure (4) gives us more clarity on this graphically.
