Question

The metallic spheres of radii 1 cm and 3 cm are given charges $-1\times {{10}^{-2}}C\text{ and 5}\times \text{1}{{\text{0}}^{-2}}C$, respectively. If they are connected by a conducting wire, the final charge on the bigger sphere will be –

& \text{A) 2}\times \text{1}{{\text{0}}^{-2}}C \\\ & \text{B) 3}\times \text{1}{{\text{0}}^{-2}}C \\\ & \text{C) 4}\times \text{1}{{\text{0}}^{-2}}C \\\ & \text{D) }1\times \text{1}{{\text{0}}^{-2}}C \\\ \end{aligned}$$

Answer 1

We need to distribute the given charges on the two spheres of different radii. For this, we need to understand the relation between the charges, the radius and other factors which govern the phenomenon such as the potential on the spheres.

Complete answer:
We are given two metallic spheres of radius 1 cm and 3 cm. It is said that there is charge on each of them of $-2\times {{10}^{-2}}C\text{ and }$ $\text{5}\times \text{1}{{\text{0}}^{-2}}C$ respectively as we can see from the figure.

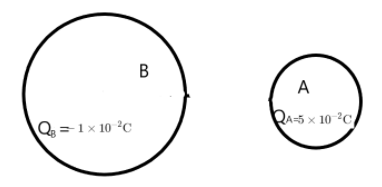
Then the two spheres are connected by a conducting wire as shown below.

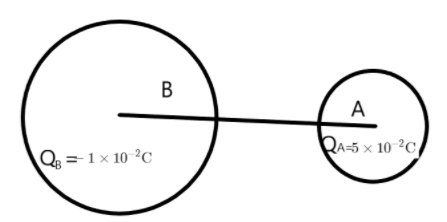
We need to find the charge on each of the spheres after this connection is made. We know that the two spheres will attain equal potentials to maintain equilibrium when the connection is made. i.e., the two spheres will be in equal potential regardless of their radius. From this information we can find the relation between the charge and the radius of the spheres.
First of all, we can find the total charge in the system by algebraic addition of the charges on each of the spheres initially,

& {{Q}_{total}}={{Q}_{A}}+{{Q}_{B}} \\\ & \Rightarrow {{Q}_{total}}=-1\times {{10}^{-2}}C\text{ + 5}\times \text{1}{{\text{0}}^{-2}}C \\\ & \Rightarrow {{Q}_{total}}=4\times {{10}^{-2}}C \\\ \end{aligned}$$ Now, we can use the formula for potential given as – $$V=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Q}{r}$$ Let us now equate the potential of the two spheres. Let us consider the charge after connecting on sphere A as $${{Q}_{1}}$$and on B as $${{Q}_{2}}$$. The relation between the radius and charge can be given as – $$\begin{aligned} & {{V}_{A}}={{V}_{B}} \\\ & \Rightarrow \dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{Q}_{A}}}{{{R}_{A}}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{Q}_{B}}}{{{R}_{B}}} \\\ & \Rightarrow \dfrac{{{Q}_{A}}}{{{Q}_{B}}}=\dfrac{{{R}_{A}}}{{{R}_{B}}} \\\ \end{aligned}$$ It is given that – $$\begin{aligned} & {{R}_{A}}=1\times {{10}^{-2}}cm \\\ & {{R}_{B}}=3\times {{10}^{-2}}cm \\\ \end{aligned}$$ We can find the ratio of charge on the spheres as – $$\dfrac{{{Q}_{A}}}{{{Q}_{B}}}=\dfrac{{{R}_{A}}}{{{R}_{B}}}=\dfrac{1}{3}$$ The charge on each of the sphere is given as – $$\begin{aligned} & \dfrac{{{Q}_{A}}}{{{Q}_{B}}}=\dfrac{1}{3} \\\ & \Rightarrow 3{{Q}_{A}}={{Q}_{B}} \\\ & \Rightarrow {{Q}_{A}}+{{Q}_{B}}={{Q}_{total}} \\\ & \Rightarrow {{Q}_{A}}+3{{Q}_{A}}={{Q}_{total}} \\\ & \Rightarrow {{Q}_{A}}=\dfrac{{{Q}_{total}}}{4}=\dfrac{4\times {{10}^{-2}}}{4} \\\ & \therefore {{Q}_{A}}=1\times {{10}^{-2}}C \\\ & \text{Also,} \\\ & \therefore {{\text{Q}}_{B}}=3\times {{10}^{-2}}C \\\ \end{aligned}$$ The required charge on the big sphere is $$3\times {{10}^{-2}}C$$. **The correct answer is option B.** **Note:** The charge on the spheres in a system of metallic spheres connected by conducting wires is dependent on the radius of the sphere under consideration. The potential differences between any two points in the system should be zero to be at equilibrium.