Question

The medians AD and BE of a triangle with vertices $A(0,b)$, $B(0,0)$ and $C(a,0)$ are perpendicular to each other if,
a) $a = \sqrt 2 b$
b) $a = - \sqrt 2 b$
c) Both (a) and (b)
d) none of these

Answer 1

Here in this question we have to determine the equation for perpendicularity. So first by considering the vertices of the triangle we determine the value of the mid points of the line. Since they are perpendicular, we know the condition: ${m_1}.{m_2} = - 1$. Then on simplification we obtain the required solution for the given question.

Complete step by step answer:
Considering the given question, ABC is a triangle with vertices $A(0,b)$, $B(0,0)$ and $C(a,0)$. The AD and BE are medians, this means the line AD is perpendicular to the line BC and line BE is perpendicular to the line AC.

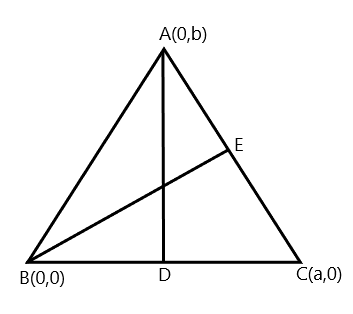
Now we determine the value of D and E. Since they are midpoints of line, we can use midpoint formula i.e., $\left( {\dfrac{{{x_2} - {x_1}}}{2},\dfrac{{{y_2} - {y_1}}}{2}} \right)$, where ${x_1} = 0,{x_2} = a,\,{y_1} = 0,\,{y_2} = 0$.
So the value of D will be
$\Rightarrow \left( {\dfrac{{a - 0}}{2},\dfrac{{0 - 0}}{2}} \right)$
On simplifying we have
$\Rightarrow \left( {\dfrac{a}{2},0} \right)$
So now we determine the value of E and it will be, Here the values are ${x_1} = 0,{x_2} = a,\,{y_1} = b,\,{y_2} = 0$
On substituting in the formula we have
$\Rightarrow \left( {\dfrac{{a - 0}}{2},\dfrac{{0 - b}}{2}} \right)$
On simplifying we have
$\Rightarrow \left( {\dfrac{a}{2},\dfrac{{ - b}}{2}} \right)$
We have determined the value of mid points. Now we have to check the condition that these two lines are perpendicular.
As we know that if two are perpendicular to each other then the product of their slope will be equal to -1.
Now we determine the slope. This is defined or given by $m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$
The slope of AD
$\Rightarrow {m_1} = \dfrac{{0 - b}}{{\dfrac{a}{2} - 0}}$
On simplifying we have
$\Rightarrow {m_1} = \dfrac{{ - b}}{{\dfrac{a}{2}}}$
On taking reciprocal we have
$\Rightarrow {m_1} = - b \times \dfrac{2}{a}$
$\Rightarrow {m_1} = \dfrac{{ - 2b}}{a}$
The slope of BE
$\Rightarrow {m_2} = \dfrac{{\dfrac{b}{2} - 0}}{{\dfrac{a}{2} - 0}}$
On simplifying we have
$\Rightarrow {m_1} = \dfrac{{\dfrac{b}{2}}}{{\dfrac{a}{2}}}$
On taking reciprocal we have
$\Rightarrow {m_2} = \dfrac{b}{2} \times \dfrac{2}{a}$
$\Rightarrow {m_2} = \dfrac{b}{a}$
The condition for the perpendicular is ${m_1}.{m_2} = - 1$
On substituting the slopes values we have
$\Rightarrow \dfrac{{ - 2b}}{a} \times \dfrac{b}{a} = - 1$
On multiplying we have
$\Rightarrow \dfrac{{ - 2{b^2}}}{{{a^2}}} = - 1$
$\Rightarrow - 2{b^2} = - {a^2}$
Cancelling the minus sign we have
$\Rightarrow 2{b^2} = {a^2}$
Taking the square root on both sides we have
$\Rightarrow a = \pm \sqrt 2 b$
Therefore, option (c) is the correct option.

Note:
When the points of triangle is given we can determine the slope of the line, that is given by Slope of a line = $\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$. In geometry, a median of a triangle is a line segment joining a vertex to the midpoint of the opposite side, thus bisecting that side. Every triangle has exactly three medians, one from each vertex, and they all intersect each other at the triangle's centroid.