Question

The maximum number of sets obtainable from A and B by applying union and difference operations is
A.5
B.6
C.7
D.8

Answer 1

Here, we have to find the maximum number of sets which are obtainable from A and B by applying union and difference operations. We will draw the Venn diagram of A and B to solve this question. We will write all the maximum possible number of sets which are obtainable by applying union and difference operations.

Complete step-by-step answer:
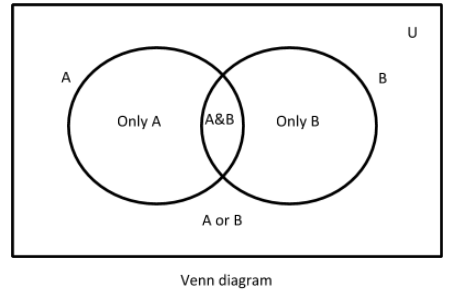
First of all, we would draw a Venn diagram of A and B.
Now, from the Venn diagram, clearly, A and B sets are divided into 3 different parts, i.e.
First part $=$Only A $=$A$-$B
Second part $=$A & B$=$A$\cap$B
Third part $=$Only B$=$B$-$A
Now, the maximum number of sets which can be obtained from A and B i.e. from these three areas would either contain only one area or two or all the three of them.
Hence, the maximum number of sets possible$=$ ${2^3} = 8$
The possible sets are:
1.An empty set $=$ \left\\{ {} \right\\}
An empty set is a subset of every set. It contains no elements.
2.A (as a whole)
This includes the first and second part.
3.B (as a whole)
This includes the second and third part.
4. A$-$B
This is the first part itself.
5.A$\cap$B
This is the second part itself.
6.B$-$A
This is the third part itself.
7.A $\cup$B
This contains all the three parts as (A $\cup$B) $=$A$+$B$-$( A$\cap$B)
(A$-$ B) $\cup$ (B$-$ A) (either/or set)
This contains the first and the third part.
So, now, if we see the small sentences carefully (which are mentioned above) then, it shows that all the possible sets have been included.
Hence, the maximum number of sets obtainable from A and B by applying union and difference operations is 8 .

Therefore, option D is the correct answer.

Note: We should know how to draw a Venn diagram, what are the different areas present in the Venn diagram known as and what they represent. Also, let’s say, if a set has 4 elements then, the number of possible subsets of that set is ${2^4} = 16$.
Hence, if a set has $n$ elements then the possible subsets are ${2^n}$ .
In this question, the sets A and B could be divided into 3 different parts (as shown in the Venn diagram).
Hence, the maximum number of sets obtainable from A and B by applying union and difference operations is
${2^3} = 8$ .