Question

The maximum number of points of intersection of five lines and four circles is
a. 60
b. 72
c. 62
d. None of these

Answer 1

Hint: In order to solve this question, we should know that for maximum intersection we will consider two figures crossing each other and not touching each other. Also, we have to remember that for choosing r out of n items irrespective of their orders, we can use the formula of combination, that is, $^{n}{{C}_{r}}=\dfrac{n!}{r!\left( n-r \right)!}$. By using these concepts we will solve this question.

Complete step-by-step answer:
In this question, we have been asked to find the maximum number of points of intersection of five lines and four circles. For that, we will consider the crossing of two figures and not the touching of two figures because touching any two figures will give less points than crossing of two figures.

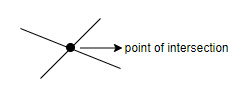
Now, we know that when two lines intersect, the maximum possible point of intersection will be one. So, for line-line intersection, we have to choose 2 out of 5 lines which we can do by using the formula of combination, which is used to choose r out of n items, that is $^{n}{{C}_{r}}=\dfrac{n!}{r!\left( n-r \right)!}$. So, for n = 5 and r = 2, we will get,
$\begin{aligned} & ^{5}{{C}_{2}}=\dfrac{5!}{2!\left( 5-2 \right)!} \\\ & ^{5}{{C}_{2}}=\dfrac{5!}{2!3!} \\\ & ^{5}{{C}_{2}}=\dfrac{5\times 4\times 3!}{2!3!}=\dfrac{5\times 4}{2}=10 \\\ & {{\therefore }^{5}}{{C}_{2}}=10 \\\ \end{aligned}$
Hence, the maximum number of points of intersection of 2 lines is 10 points.
Now, in the same way, we will calculate the points of intersection of 2 circles

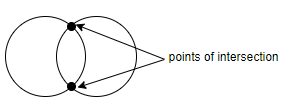
Now, we know that we get 2 points when 2 circles intersect each other and we have to choose 2 out of 4 circles. So, we can say that the maximum number of points of intersection of the circles can be given as,
$\begin{aligned} & \Rightarrow 2{{\times }^{4}}{{C}_{2}} \\\ & =2\times \dfrac{4!}{2!\left( 4-2 \right)!} \\\ & =2\times \dfrac{4!}{2!2!} \\\ & =2\times \dfrac{4\times 3\times 2!}{2!2!} \\\ & =2\times \dfrac{4\times 3}{2} \\\ & =2\times 6 \\\ & =12 \\\ \end{aligned}$
Now, we will consider the case of line-circle intersection.

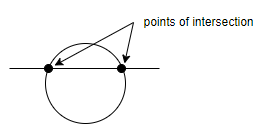
Now, from the figure, we can see that when a line intersects a circle, it gives 2 points of intersection and we have to choose 1 circle out of 4 and 1 line out of 5. So, we can write the maximum points of line circle intersection as,

& 2{{\times }^{4}}{{C}_{1}}{{\times }^{5}}{{C}_{1}} \\\ & =2\times \dfrac{4!}{1!\left( 4-1 \right)!}\times \dfrac{5!}{1!\left( 5-1 \right)!} \\\ & =2\times \dfrac{4!}{1!3!}\times \dfrac{5!}{1!4!} \\\ & =2\times \dfrac{4\times 3!}{1\times 3!}\times \dfrac{5\times 4!}{1\times 4!} \\\ & =2\times 4\times 5 \\\ & =40 \\\ \end{aligned}$$ Hence, the maximum points of intersection of 5 lines and 4 circles can by calculated by adding the points of line-line intersection, circle-circle intersection and line-circle intersection. So, we get, 10 + 12 + 40 = 62 points Therefore, the maximum points of intersection of 5 lines and 4 circles are 62. Hence, option (c) is the correct answer. Note: The possible mistake one can make in this question is by not including line-line intersection, circle-circle intersection or line-circle intersection. Also, one can think of solving this question by making a figure which includes all the conditions given in the question which will help us get the right answer.