Question

The maximum number of electrons that can have principal quantum number, n = 3, and spin quantum number, $\mathrm{m}_{\mathrm{s}}= -1 / 2$ is:
(A)7
(B)8
(C)9
(D) 10

Answer 1

In any nth orbit there can have a maximum of $2 n^{2}$ electrons. Out of which half of them has spin quantum numbers, $\mathrm{m}_{\mathrm{s}}=-1 / 2$ and the other half as $\mathrm{m}_{\mathrm{s}}=+1 / 2$

Complete step by step solution:
-The principal quantum number, which is given by symbol n, has positive values like, 1,2,3,....,etc. It determines the size and the energy of the orbital. Orbitals that have the same value of the principal quantum number form a shell.
-The azimuthal quantum number is represented by l and describes the three-dimensional shape of the orbital occupied by the electron. The l can take values from $0$ to $(n-1)$.
-The spin quantum number is represented as ms. It refers to the two possible orientations of the spin axis of an electron and can take the values $+1 / 2$ and $-1 / 2$ for a given n. An electron spins around its own axis while moving around the nucleus in its orbital.The $+1 / 2$ corresponds to the vector $\uparrow$ and $-1 / 2$ corresponds to the vector $\downarrow$.
-Now, let us approach the question.
We have $n=3$.
Thus, $l=0,1,2$.
Thus, there are three orbitals associated i.e., 3s,3p and 3d.
Now, they are completely filled.

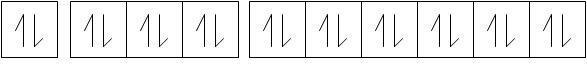
Now, it is evident that in any nth orbit, there are a maximum of $2 n^{2}$ electrons.
Thus when n=3, maximum number of electrons = 18.
Now, half of these electrons have spin quantum as $+1 / 2$ and $-1 / 2$.
-Thus, 9 electrons have $\mathrm{m}_{\mathrm{s}}=+1 / 2$ and 9 electrons have $\mathrm{m}_{\mathrm{s}}=-1 / 2$

Clearly, the answer is (C).

Note: Atomic spectra have shown that electrons in atoms occupy discrete energy states or energy levels. The quantum mechanical model allows only certain combinations of quantum numbers to describe these states. The principal quantum number cannot be zero.