Question

The maximum distance between interatomic lattice planes is $15\;A^{\circ}$. The maximum wavelength of x-rays which are diffracted by this crystal will be:
A. $15\;A^{\circ}$
B. $20\;A^{\circ}$
C. $30\;A^{\circ}$
D. $45\;A^{\circ}$

Answer 1

We need to arrive at an expression that relates the distance between the lattice planes and the wavelength of light incident on them. For this, consider two rays striking two adjacent lattice planes and determine the difference in the path length travelled by the two rays, as the ray hitting a lower plane travels more distance. We know that for constructive interference, the difference in path length is generally an integral multiple of the wavelength of incident light. Equate the two expressions thus obtained to arrive at the required expression, and plug in the given values. Remember to use the upper limit for quantities in the resultant equation whose values are not explicitly mentioned since we have to find the maximum wavelength.

Formula used:
Bragg’s Law: $2d\sin\theta =n \lambda$

Complete step-by-step answer:
Let us begin by establishing a relation between the distance between interatomic lattice planes and the wavelength of light incident on them.

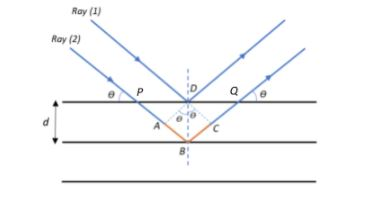
Given that x-rays of wavelength, say $\lambda$ are incident on a crystal as shown in the figure, consider two rays, Ray 1 and Ray 2, striking two adjacent planes that are at a distance$\;d$ apart. Let the rays make an angle $\theta$ with the vertical as they strike the lattice planes. We see that Ray 2 travels more distance to hit the inner plane than Ray 1 that hits the closest plane. We shall now find the path difference between the two rays.
From the diagram, we see that the path difference is $\Delta P = AB +BC$.
We see that $\angle APD = \theta$ and $\angle DAP = 90^{\circ}$, and from $\Delta APD$, we have:
$\angle ADP = 180 - (90 + \theta) = 90 -\theta$ (Since the sum of all angles in a $\Delta = 180^{\circ}$)
Now, from the figure, since $\angle PDB = 90^{\circ}$ and $\angle ADP = 90+\theta$,
$\angle ADB= \angle PDB - \angle ADP = 90 – (90 -\theta) = \theta$
Therefore, from right angled $\Delta ADB$:
$\sin\theta = \dfrac{AB}{DB} \Rightarrow AB = DB\sin\theta = d\sin\theta$
Similarly, $BC = d\sin\theta$, therefore, path difference:
$\Delta P = AB+BC = d\sin\theta + d\sin\theta = 2d\sin\theta$
Now, for constructive interference, the difference in path length is an integral number of the wavelength of incident light, i.e.,
$\Delta P = n\lambda$, where n denotes the order of diffraction that is usually set to unity.
Equating the above two expressions, we get:
$n\lambda = 2d\sin\theta$
This is nothing but Bragg’s law for constructive interference.
$\Rightarrow \lambda = \dfrac{2d\sin\theta}{n}$
Now, we are given that the maximum distance between the lattice planes in $d_{max} = 15\;A^{\circ} = 15 \times 10^{-10}\;m$. Therefore, the maximum wavelength of x-rays which are diffracted by this crystal will be:
$\lambda_{max} = \dfrac{2d_{max}\sin\theta_{max}}{n_{max}}$
We know that the intensity maxima is obtained at $n_{max}=1$, and the maximum value of $\sin\theta$ will be at $\theta_{max} = 90^{\circ}$, since $\sin90^{\circ} = 1$. Plugging this into our wavelength expression, we get:
$\lambda_{max} = \dfrac{2 \times 15 \times 10^{-10} \times 1 }{1} = 30 \times 10^{-10}\;m = 30\;A^{\circ}$

So, the correct answer is “Option C”.

Note: X-ray diffraction is a technique that is generally used to determine the crystallographic structure of a material by observing the diffraction pattern thus obtained when x-rays are made incident on a crystal. By measuring the angles and intensities of these diffracted beams, a crystallographer can produce a three-dimensional picture of the density of electrons within the crystal and consequently determine the nature of the crystal. Thus, it is important to note that the x-rays impinging on the crystals get diffracted not by the planes themselves but by the constituents of the planes, which are usually electrons arranged in regular arrays within the crystal structure.