Question

The maximum area of the rectangle that can be inscribed in a circle of radius r is –

• A. pr²
• B. r²
• C.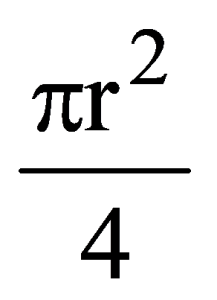
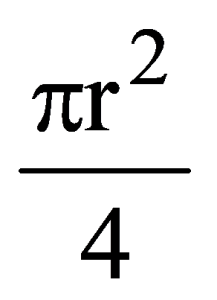
• D. ) 2r²

Answer 1

)

Sol. Area of rectangle

D = 2 × 2x

D = 4x $\sqrt { \left( r ^ { 2 } - x ^ { 2 } \right) }$

or D² = 16 x² (r² – x²)

= (16r²x² – 16x⁴) = l (say)

\ = 32r²x – 16x³

Now = 0, \ x =

= 32r² – 192x²

$\left. \frac { d \lambda ^ { 2 } } { d x ^ { 2 } } \right| _ { x = \frac { r } { \sqrt { 2 } } }$ = – 64r² < 0

Hence area maximum when x =

\ Maximum area =

= · = 2r².

Alternate Method : In a circle maximum are a rectangle is always square

Whose area = = = 2r².