Question

The maximum and minimum values of the function $y = {x^3} - 3{x^2} + 6$ are
A) 2, 0
B) 6, 0
C) 6, 2
D) 4, 2

Answer 1

Here, we will first calculate the first-order derivative $\dfrac{{dy}}{{dx}}$ of the given function $y$ and then take it equals to 0 to find the critical points. Then we will find the sign of the second-order derivative $\dfrac{{{d^2}y}}{{d{x^2}}}$ at the obtained critical points. If the sign of second differentiation is negative, then the function has a point of maxima and if the second differentiation is positive, the function has a point of minima. Substitute the values in the given equation to find the required values.

Complete step by step solution: We are given that the function $y = {x^3} - 3{x^2} + 6$.

We know that the point of maximum or minimum is calculated by taking the differentiation $\dfrac{{dy}}{{dx}}$ of the given function $y$ equals to 0 and then finding the sign of the second differentiation $\dfrac{{{d^2}y}}{{d{x^2}}}$. If the second differentiation is negative, the function has a point of maxima and if the second differentiation is positive, the function has a point of minima.

Differentiating the above function with respect to $x$, we get

$$\Rightarrow \dfrac{{dy}}{{dx}} = \dfrac{d}{{dx}}\left( {{x^3} - 3{x^2} + 6} \right) \\\ \Rightarrow \dfrac{{dy}}{{dx}} = 3{x^2} - 6x{\text{ ......eq.(1)}} \\\$$

Taking $\dfrac{{dy}}{{dx}} = 0$ to find the critical point in the above equation, we get

$$\Rightarrow 3{x^2} - 6x = 0 \\\ \Rightarrow 3x\left( {x - 2} \right) = 0 \\\$$

$\Rightarrow 3x = 0$ or $x - 2 = 0$

Simplifying the above equations, we get

$\Rightarrow x = 0$ or $x = 2$

Therefore, $x = 0$ and $x = 2$ are the critical points of the given equation.
Differentiating the equation $(1)$ using the product rule, we get

$$\Rightarrow \dfrac{{{d^2}y}}{{d{x^2}}} = \dfrac{d}{{dx}}\left( {3{x^2} - 2x} \right) \\\ \Rightarrow \dfrac{{{d^2}y}}{{d{x^2}}} = 6x - 2 \\\$$

First, replacing 0 for $x$ in the above equation, we get

$$\Rightarrow {\left. {\dfrac{{{d^2}y}}{{d{x^2}}}} \right|_{x = 0}} = 6\left( 0 \right) - 2 \\\ \Rightarrow {\left. {\dfrac{{{d^2}y}}{{d{x^2}}}} \right|_{x = 0}} = - 2 \\\$$

Since $- 2$ is negative, the given function has a point of maxima at $x = 0$.
We will now find the maximum value of the function at point $x = 0$ by substituting it in the given equation.

$$\Rightarrow {\left. y \right|_{x = 0}} = {0^3} - 3{\left( 0 \right)^2} + 6 \\\ \Rightarrow {\left. y \right|_{x = 0}} = 0 - 3\left( 0 \right) + 6 \\\ \Rightarrow {\left. y \right|_{x = 0}} = 0 - 0 + 6 \\\ \Rightarrow {\left. y \right|_{x = 0}} = 6 \\\$$

Thus, the maximum value of the given function is 6.

Now, replacing 2 for $x$ in the above equation, we get

$$\Rightarrow {\left. {\dfrac{{{d^2}y}}{{d{x^2}}}} \right|_{x = 2}} = 6\left( 2 \right) - 2 \\\ \Rightarrow {\left. {\dfrac{{{d^2}y}}{{d{x^2}}}} \right|_{x = 2}} = 12 - 2 \\\ \Rightarrow {\left. {\dfrac{{{d^2}y}}{{d{x^2}}}} \right|_{x = 2}} = 10 \\\$$

Since $10$ is positive, the given function has a point of minima at $x = 2$.
We will now find the minimum value of the function at point $x = 2$ by substituting it in the given equation.

$$\Rightarrow {\left. y \right|_{x = 2}} = {2^3} - 3{\left( 2 \right)^2} + 6 \\\ \Rightarrow {\left. y \right|_{x = 2}} = 8 - 3\left( 4 \right) + 6 \\\ \Rightarrow {\left. y \right|_{x = 2}} = 8 - 12 + 6 \\\ \Rightarrow {\left. y \right|_{x = 2}} = 2 \\\$$

Thus, the minimum value of the given function is 2.

Therefore, the maximum value of the given equation is 6 and the minimum value of the given equation is 2.

Hence, option C is correct.

Note: In solving these types of questions, you should be familiar with the steps to find the point of maxima and the point of minima. We can also find the values, where $\dfrac{{dy}}{{dx}}$ equals zero at a certain point, it means that the slope of the tangent at that point is zero. So by finding the sign of $\dfrac{{dy}}{{dx}}$ in the neighbourhood of that point, then we can find the point of maxima and minima. If the sign of the derivative changes from positive to negative, then at that point it will have maxima otherwise minima.

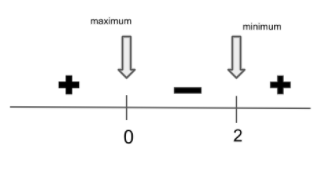
Thus, 0 is the point of maxima and 2 is the point of minima.

We will now find the maximum value of the function at point $x = 0$ by substituting it in the given equation.

$$\Rightarrow {\left. y \right|_{x = 0}} = {0^3} - 3{\left( 0 \right)^2} + 6 \\\ \Rightarrow {\left. y \right|_{x = 0}} = 0 - 3\left( 0 \right) + 6 \\\ \Rightarrow {\left. y \right|_{x = 0}} = 0 - 0 + 6 \\\ \Rightarrow {\left. y \right|_{x = 0}} = 6 \\\$$

This implies that the maximum value of the given function is 6.
We will then find the minimum value of the function at point $x = 2$ by substituting it in the given equation, we get

$$\Rightarrow {\left. y \right|_{x = 2}} = {2^3} - 3{\left( 2 \right)^2} + 6 \\\ \Rightarrow {\left. y \right|_{x = 2}} = 8 - 3\left( 4 \right) + 6 \\\ \Rightarrow {\left. y \right|_{x = 2}} = 8 - 12 + 6 \\\ \Rightarrow {\left. y \right|_{x = 2}} = 2 \\\$$

Thus, the minimum value of the given function is 2.
Hence, option C is correct again.