Question

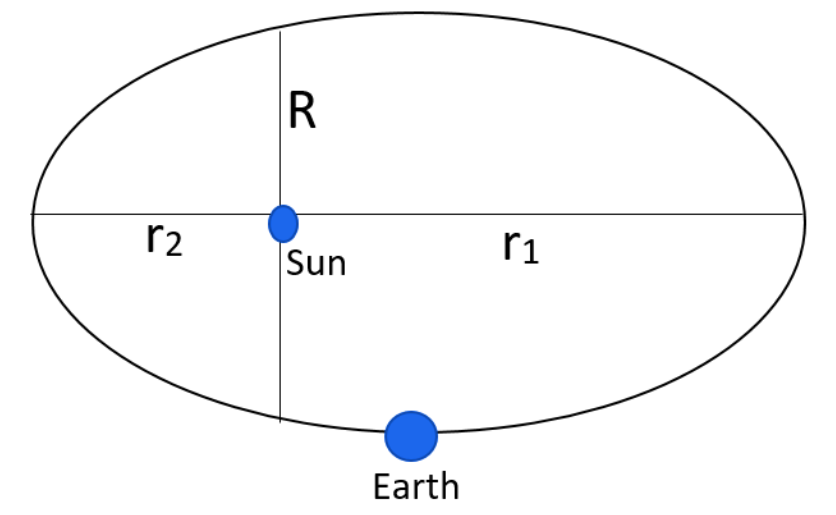
The maximum and minimum distance of earth from the sun are ${{r}_{1\text{ }}}and\text{ }{{r}_{2}}$ ​ respectively. How can we find the distance of earth from the sun if its position vector is perpendicular to the major axis of its orbit?
$\begin{aligned} & A.\dfrac{{{r}_{1}}+{{r}_{2}}}{4} \\\ & B.\dfrac{{{r}_{1}}+{{r}_{2}}}{{{r}_{1}}-{{r}_{2}}} \\\ & C.\dfrac{2{{r}_{1}}{{r}_{2}}}{{{r}_{1}}+{{r}_{2}}} \\\ & D.\dfrac{{{r}_{1}}+{{r}_{2}}}{3} \\\ \end{aligned}$

Answer 1

The earth is rotating the sum in an elliptical orbit. Find out the equation for position of a particle with perpendicular distance from focus using the eccentricity. By the use of this formula, find out the maximum and minimum distance and compare them with the original value mentioned in the question. Add both these rearranged equations in order to get the distance from the perpendicular to the principal axis.

Complete step by step answer:
let us assume that the eccentricity of the elliptical orbit is given as $e$,
Then we can find the position of the particle with perpendicular distance from focus.
That is we can write that,
$r=\dfrac{1}{\left( 1+e\cos \theta \right)}$
Using this equation, we can write the maximum and minimum distance. For maximum distance the angle persisting will be
$\theta =180{}^\circ$
Therefore the cosine term will be negative of one. Hence we can write that,
The maximum distance,
${{r}_{1}}=\dfrac{1}{\left( 1-e \right)}$
Rearranging this equation will give,
$\left( 1-e \right)=\dfrac{1}{{{r}_{1}}}$
For the minimum distance, the angle present there will be zero. Therefore cosine terms will be one.
The minimum distance from the sun is given as,
${{r}_{2}}=\dfrac{1}{\left( 1+e \right)}$
Rearranging this equation will give,
$\left( 1+e \right)=\dfrac{1}{{{r}_{2}}}$
Now let us add both these rearranged equations together,
$2=\dfrac{1}{{{r}_{1}}}+\dfrac{1}{{{r}_{2}}}$
Cross multiplying the fractional values,
$2=1\dfrac{\left( {{r}_{1}}+{{r}_{2}} \right)}{{{r}_{1}}{{r}_{2}}}$
As we have to find the distance of earth from the sun if its position vector is perpendicular to the major axis of its orbit, the value will be equal to one. Therefore after rearranging,
$1=2\dfrac{{{r}_{1}}{{r}_{2}}}{\left( {{r}_{1}}+{{r}_{2}} \right)}$
Therefore the distance from a perpendicular to the major axis is obtained.

So, the correct answer is “Option C”.

Note: The eccentricity of an ellipse is given as the ratio of the distance found in between the centre of the ellipse and each focus to the semi major axis length a circle is having eccentricity zero. That means the eccentricity is the measure of how the curve is varying from the circle.