Question

The maximum and minimum distance between a convex lens and an object, for the magnification of a real image to be greater than one are
A) 2f and f
B) F and zero
C) $\infty$ and 2f
D) 4f and 2f

Answer 1

In order to find the maximum and minimum distance between a convex lens and an object, we will start with the magnification of the lens which is negative for real image and then using lens formula $\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$we will substitute the value of v(image position) in magnification and reciprocate to find desired solution.

Step by step solution:
Step 1:
Before coming to the question let us see what a convex lens is
A convex lens is also called a converging lens because it makes parallel light rays passing through it bend inward and meet (converge) at a spot just beyond the lens known as the focal point. Photo: A convex lens makes parallel light rays converge (come together) at the focal point or focus.

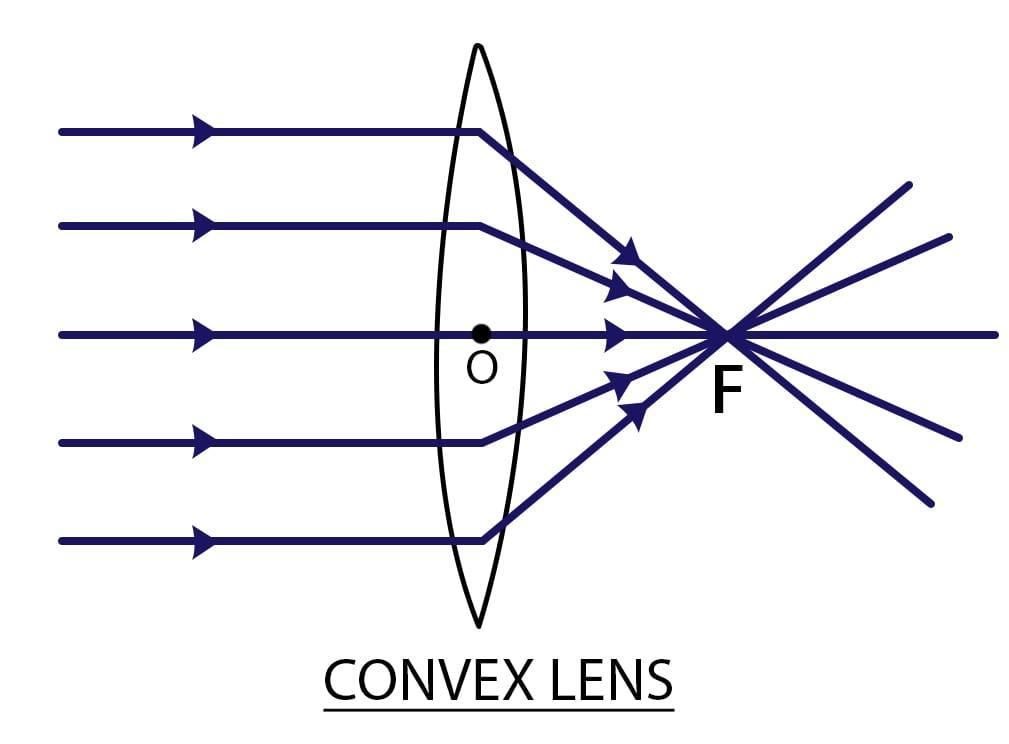
Step 2:
A convex lens can form virtual as well as real images, so the magnification produced by a convex lens can be either positive or negative. Magnification is positive for virtual images and negative for real images.
For magnification of real image to be greater than 1 for lens,
$\rightarrow - \infty < \dfrac{v}{u} < \- 1$ Here, $\dfrac{v}{u}$ is the magnification of the lens.
From the equation of the lens we can write $\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$ … (1) where u is the position of object, v is the position of image and f is the focal length.
Rewriting equation (1) $\Rightarrow v = \dfrac{{uf}}{{u + f}}$ …… (2)
Putting the value of (2) in magnification of lens
We get, $- \infty < \dfrac{f}{{u + f}} < \- 1$ ……. (3)
Now to get the solution we will reciprocate the above equation (3)
This implies$0 > \dfrac{u}{f} + 1 > - 1$ $\Rightarrow - 1 > \dfrac{u}{f} > - 2$
The limits of maximum and minimum distance will be$- 2f < u < \- f$
Hence maximum and minimum distance between a convex lens and an object is 2f and f

Option A is the correct answer.

Additional information:
Some convex lens uses are given below.
-Used in magnifying glasses. One of the most direct and simplest uses of a convex lens is in a magnifying glass.
-Convex lenses are used in eyeglasses.
-Uses of convex lenses in cameras.
-Used in microscopes.

Note: In simple words a convex lens forms an image by refracting light rays. Light rays reflected from an object are refracted when they enter the lens and again when they leave the lens. They meet to form the image.