Question

The maximal electric field intensity on the axis of a uniformly charged ring of charge q and radius will be?
$\left( a \right)\dfrac{1}{4\pi {{\varepsilon }_{\text{o}}}}\dfrac{q}{\left( 3\sqrt{3} \right){{R}^{2}}}$
$\left( b \right)\dfrac{1}{4\pi {{\varepsilon }_{\text{o}}}}\dfrac{2q}{3{{R}^{2}}}$
$\left( c \right)\dfrac{1}{4\pi {{\varepsilon }_{\text{o}}}}\dfrac{2q}{\left( 3\sqrt{3} \right){{R}^{2}}}$
$\left( d \right)\dfrac{1}{4\pi {{\varepsilon }_{\text{o}}}}\dfrac{3q}{\left( 2\sqrt{2} \right){{R}^{2}}}$

Answer 1

As there is a uniformly charged ring so the charge will be equally spread over the ring. Each charge will produce field intensity. To find maximum electric field intensity we will take differentiation of the equation of this case. After this we will substitute the value of x in the very first equation.
Formula used:
$E=\dfrac{kqx}{{{\left( {{x}^{2}}+{{R}^{2}} \right)}^{\dfrac{3}{2}}}}$ where R is radius of circle, E is electric field intensity, q is a charge and x is the distance between the center of ring and the field intensity.

Complete answer:
Electric field intensity: As the name suggests, the intensity of electric field in the form of force which is exerted on an object by a different charged object. To be more precise the field intensity on a unit charge is the force that is exerted by that unit charge kept under that field.

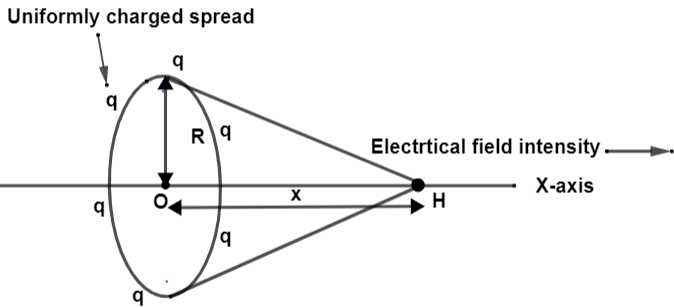
By the information given in the question we have drawn a ring with a uniform charge spread all over it. These charges produce electric field intensity at point H. Since, each charge is involved in the production of the field, so basically the ring is producing the electric field intensity at point H. This field intensity is made on the x-axis. If the ring was made perpendicular to the y-axis thus the field intensity would also be produced on the y-axis.
Suppose the field intensity is represented by the formula $E=\dfrac{kqx}{{{\left( {{x}^{2}}+{{R}^{2}} \right)}^{\dfrac{3}{2}}}}$….(i).

To find the intensity produced on the very small part of the x-axis then, it will be represented by dx. Now, we will calculate the field intensity at dx only. Therefore, we will get

$\dfrac{dE}{dx}=kq\dfrac{d}{dx}\left( \dfrac{x}{{{\left( {{x}^{2}}+{{R}^{2}} \right)}^{\dfrac{3}{2}}}} \right)$
At this step we will apply differentiation formula $d\left( \dfrac{u}{v} \right)=\dfrac{vdu-udv}{{{v}^{2}}}$ to get,
\Rightarrow \dfrac{dE}{dx}=kq\left\\{ \dfrac{\left[ {{\left( {{x}^{2}}+{{R}^{2}} \right)}^{\dfrac{3}{2}}} \right]\dfrac{dx}{dx}-x\dfrac{d\left[ {{\left( {{x}^{2}}+{{R}^{2}} \right)}^{\dfrac{3}{2}}} \right]}{dx}}{{{\left( {{\left( {{x}^{2}}+{{R}^{2}} \right)}^{\dfrac{3}{2}}} \right)}^{2}}} \right\\}
\Rightarrow \dfrac{dE}{dx}=kq\left\\{ \dfrac{\left[ {{\left( {{x}^{2}}+{{R}^{2}} \right)}^{\dfrac{3}{2}}} \right]-x\left( \dfrac{3}{2}{{\left( {{x}^{2}}+{{R}^{2}} \right)}^{\dfrac{3}{2}-1}}\left( \dfrac{d\left( {{x}^{2}} \right)}{dx} \right) \right)}{{{\left( {{\left( {{x}^{2}}+{{R}^{2}} \right)}^{\dfrac{3}{2}}} \right)}^{2}}} \right\\}
\Rightarrow \dfrac{dE}{dx}=kq\left\\{ \dfrac{\left[ {{\left( {{x}^{2}}+{{R}^{2}} \right)}^{\dfrac{3}{2}}} \right]-x\left( \dfrac{3}{2}{{\left( {{x}^{2}}+{{R}^{2}} \right)}^{\dfrac{1}{2}}}\left( 2x \right) \right)}{{{\left( {{\left( {{x}^{2}}+{{R}^{2}} \right)}^{\dfrac{3}{2}}} \right)}^{2}}} \right\\}

Now, to find the maximum field intensity it is a must to put dE = 0. Therefore,
\begin{aligned} & \Rightarrow \dfrac{dE}{dx}=0 \\\ & \Rightarrow kq\left\\{ \dfrac{\left[ {{\left( {{x}^{2}}+{{R}^{2}} \right)}^{\dfrac{3}{2}}} \right]-x\left( \dfrac{3}{2}{{\left( {{x}^{2}}+{{R}^{2}} \right)}^{\dfrac{1}{2}}}\left( 2x \right) \right)}{{{\left( {{\left( {{x}^{2}}+{{R}^{2}} \right)}^{\dfrac{3}{2}}} \right)}^{2}}} \right\\}=0 \\\ \end{aligned}
$\Rightarrow \left[ {{\left( {{x}^{2}}+{{R}^{2}} \right)}^{\dfrac{3}{2}}} \right]-x\left( \dfrac{3}{2}{{\left( {{x}^{2}}+{{R}^{2}} \right)}^{\dfrac{1}{2}}}\left( 2x \right) \right)=0$
$\Rightarrow \left[ {{\left( {{x}^{2}}+{{R}^{2}} \right)}^{\dfrac{3}{2}}} \right]=x\left( \dfrac{3}{2}{{\left( {{x}^{2}}+{{R}^{2}} \right)}^{\dfrac{1}{2}}}\left( 2x \right) \right)$
After dividing both sides by ${{\left( {{x}^{2}}+{{R}^{2}} \right)}^{\dfrac{1}{2}}}$ we get
$\Rightarrow \dfrac{\left[ {{\left( {{x}^{2}}+{{R}^{2}} \right)}^{\dfrac{3}{2}}} \right]}{{{\left( {{x}^{2}}+{{R}^{2}} \right)}^{\dfrac{1}{2}}}}=\dfrac{x\left( \dfrac{3}{2}{{\left( {{x}^{2}}+{{R}^{2}} \right)}^{\dfrac{1}{2}}}\left( 2x \right) \right)}{{{\left( {{x}^{2}}+{{R}^{2}} \right)}^{\dfrac{1}{2}}}}$
$\Rightarrow \left( {{x}^{2}}+{{R}^{2}} \right)=x\dfrac{3}{2}\left( 2x \right)$
$\Rightarrow {{x}^{2}}+{{R}^{2}}=3{{x}^{2}}$
$\Rightarrow {{R}^{2}}=3{{x}^{2}}-{{x}^{2}}$
$\Rightarrow {{R}^{2}}=2{{x}^{2}}$
$\Rightarrow {{x}^{2}}=\dfrac{{{R}^{2}}}{2}$
After applying square root our equation changes into,
$x=\pm \dfrac{R}{\sqrt{2}}$

We will put both values of x in equation (i). So,
$E=\dfrac{kq\left( \dfrac{R}{\sqrt{2}} \right)}{{{\left( {{\left( \pm \dfrac{R}{\sqrt{2}} \right)}^{2}}+{{R}^{2}} \right)}^{\dfrac{3}{2}}}}$
$\Rightarrow E=\dfrac{kq\left( \dfrac{R}{\sqrt{2}} \right)}{{{\left( \dfrac{{{R}^{2}}}{2}+{{R}^{2}} \right)}^{\dfrac{3}{2}}}}$
$\Rightarrow E=\dfrac{kq\left( \dfrac{R}{\sqrt{2}} \right)}{{{\left( \dfrac{3{{R}^{2}}}{2} \right)}^{\dfrac{3}{2}}}}$
$\Rightarrow E=\dfrac{kq\left( \dfrac{R}{\sqrt{2}} \right)}{{{\left( \dfrac{3}{2} \right)}^{\dfrac{3}{2}}}{{R}^{3}}}$
$\Rightarrow E=\dfrac{kq\dfrac{1}{{{\left( 2 \right)}^{\dfrac{1}{2}}}}}{\dfrac{{{\left( 3 \right)}^{\dfrac{3}{2}}}}{{{\left( 2 \right)}^{\dfrac{3}{2}}}}{{R}^{2}}}$
$\Rightarrow E=\dfrac{kq}{{{R}^{2}}}\dfrac{{{\left( 2 \right)}^{\dfrac{3}{2}-\dfrac{1}{2}}}}{{{\left( 3 \right)}^{\dfrac{3}{2}}}}$
$\Rightarrow E=\dfrac{kq}{{{R}^{2}}}\dfrac{2}{3\sqrt{3}}$

So, the correct answer is “Option C”.

Note:
The first point that should be understood is about the equation of the electric field intensity which can be carried out by the diagram. Since, we need to find the maximum value of the intensity so; we will find the differentiation of the equation and put that equal to 0. After solving it we will find the value of x. It is important to focus while solving the question. Since, it includes basic but important formulas, one should know about them. The solution is a bit lengthy, so we will solve it by putting most of our focus in calculations. While substituting the value of x one should put it in numerator as well as denominator both.