Question

The massless pulley P is moving vertically downwards with constant speed of 15 m/s. Find the velocity (in m/s) with which the block Q moves up at the instant shown. (All pulleys are frictionless)

Answer 1

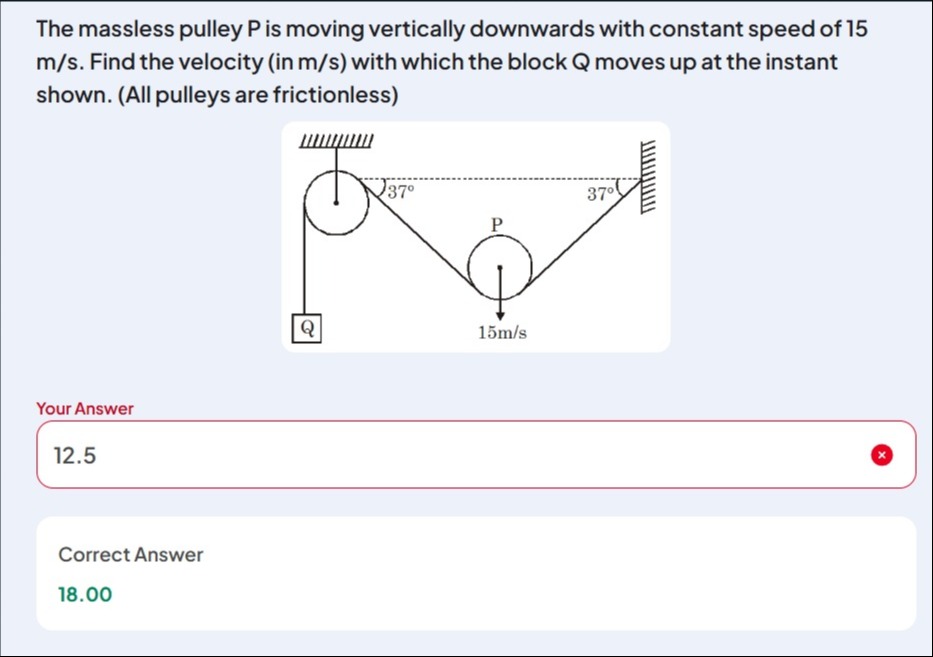
18.00

Answer 2

Let $y_P$ be the vertical position of the center of pulley P measured downwards from the horizontal line passing through the fixed pulley and the fixed support. Let $x$ be the horizontal distance from the fixed pulley (or fixed support) to the vertical line through pulley P. Due to symmetry, the horizontal distance to the fixed pulley and the fixed support are the same, say $x$.

The length of the string segment from the fixed pulley to the movable pulley P is $L_1 = \sqrt{x^2 + y_P^2}$. The length of the string segment from the movable pulley P to the fixed support is $L_2 = \sqrt{x^2 + y_P^2}$. The length of the string from the fixed pulley to block Q is $L_Q$. Let $y_Q$ be the vertical position of block Q measured upwards from some reference. Let the fixed pulley be at a fixed vertical position. The length of the string from the fixed pulley to Q is proportional to the distance of Q below the fixed pulley. Let's consider the length of the string from the fixed pulley to Q to be $L_Q$. If Q moves up with velocity $v_Q$, then the rate of decrease of this length is $v_Q$. So, $\frac{dL_Q}{dt} = -v_Q$.

The total length of the string $L = L_Q + L_1 + L_2 + \text{length of string around pulley P} = L_Q + 2\sqrt{x^2 + y_P^2} + \text{constant}$. Since the total length of the string is constant, $\frac{dL}{dt} = 0$. $\frac{dL_Q}{dt} + 2 \frac{d}{dt}(\sqrt{x^2 + y_P^2}) = 0$. $\frac{d}{dt}(\sqrt{x^2 + y_P^2}) = \frac{1}{2\sqrt{x^2 + y_P^2}} (2y_P \frac{dy_P}{dt}) = \frac{y_P}{\sqrt{x^2 + y_P^2}} \frac{dy_P}{dt}$. From the diagram, the angle between the string and the horizontal is $37^\circ$. Let $\theta = 37^\circ$. Then $\sin \theta = \frac{y_P}{\sqrt{x^2 + y_P^2}}$. So, $\frac{d}{dt}(\sqrt{x^2 + y_P^2}) = (\sin 37^\circ) \frac{dy_P}{dt}$. We are given that pulley P is moving vertically downwards with speed 15 m/s. This means $\frac{dy_P}{dt} = 15$ m/s (since $y_P$ is measured downwards). Substituting these into the equation for $\frac{dL}{dt}$: $-v_Q + 2 (\sin 37^\circ) (15) = 0$. $v_Q = 2 \times \sin 37^\circ \times 15$. We are given $\sin 37^\circ \approx 0.6$. $v_Q = 2 \times 0.6 \times 15 = 2 \times 9 = 18$ m/s.

Alternatively, consider the velocity of the point on the string. For the segment of the string from the fixed pulley to P, the velocity of the string along its length is related to the velocity of P. Let the velocity of P be $\vec{v}_P$. The velocity of the string at P is $\vec{v}_P$. The component of $\vec{v}_P$ along the string is $v_P \sin 37^\circ$. Since the string is inextensible, the speed of the string segment between the fixed pulley and P is constant along its length. Thus, the speed of the string leaving the fixed pulley towards P is $v_P \sin 37^\circ$. Similarly, for the segment of the string from P to the fixed support, the speed of the string is also $v_P \sin 37^\circ$. The string passes over the fixed pulley and is attached to block Q. The speed of block Q moving upwards is equal to the speed at which the string is pulled up over the fixed pulley. The string is pulled up from the side of P with speed $v_P \sin 37^\circ$ and also from the side of the fixed support with speed $v_P \sin 37^\circ$. Since these two segments combine at P and go over the fixed pulley, the total speed of the string going over the fixed pulley is the sum of the speeds of the two segments relative to the pulley P. However, this is not correct.

Let's use the velocity constraint along the string. Let $v_P$ be the speed of pulley P downwards. Consider the point on the string just above pulley P. Its velocity is $v_P$ downwards. The string is moving relative to the pulley. The velocity of the string along the segment connecting the fixed pulley and P has a component in the vertical direction. The velocity of the string along the direction of the string from the fixed pulley towards P is $v_s$. The vertical component of this velocity is $v_s \sin 37^\circ$. The velocity of P is $v_P$ downwards. The velocity of the string relative to P at the point where it touches P from the fixed pulley side is $v_s$ along the string. The velocity of this point on the string is the velocity of P plus the velocity of the string relative to P.

Let's go back to the length constraint method, which is more reliable. $v_Q = 2 \times \sin 37^\circ \times v_P$. Given $v_P = 15$ m/s and $\sin 37^\circ = 0.6$. $v_Q = 2 \times 0.6 \times 15 = 1.2 \times 15 = 18$ m/s.

The block Q moves up with a velocity of 18 m/s.